Question

Prove that the slope of a non-vertical line passing through the points A $\left( {{x}_{1}},{{y}_{1}} \right)$ and B $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $m=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)$.

Answer 1

Hint: To prove $m=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)$ first of all we will have to consider the two points on the Cartesian plane (x-y) and then join the points to each other and construct a right angle triangle with the distance between the points as a hypotenuse. We know that the slope of a line is equal to the tangent value of angle made by the line and x-axis in anticlockwise direction.
Complete step-by-step answer:
Let us consider the given points A $\left( {{x}_{1}},{{y}_{1}} \right)$ and B $\left( {{x}_{2}},{{y}_{2}} \right)$ in the x-y plane and the angle made by the line with x-axis in anticlockwise direction to be $'\theta '$.

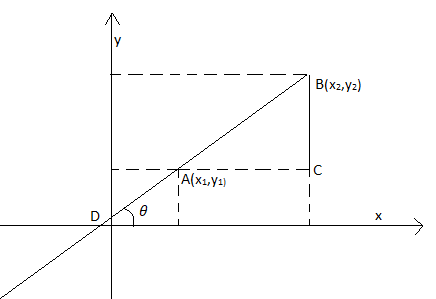
Since AC is parallel to x-axis and BD cuts them, we can say that,
$\Rightarrow \angle BAC=\theta$ as these are corresponding angles
From the figure, we can get AC and BC by subtracting the corresponding x and y coordinates of points A, B and C. A and C have the same coordinates.
$AC={{x}_{2}}-{{x}_{1}}$ and $BC={{y}_{2}}-{{y}_{1}}$
Now in triangle $\Delta ABC$, we have as follows:
$\tan A=\dfrac{BC}{AC}$
Since $\angle A=\theta$, $AC={{x}_{2}}-{{x}_{1}}$ and $BC={{y}_{2}}-{{y}_{1}}$
$\Rightarrow \tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Since we know that slope of a line (m) is also equal to the tangent value of angle made by the line with x-axis in anticlockwise direction.
$\Rightarrow slope(m)=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\tan \theta$
Therefore, it is proved that the slope of a line passing through A $\left( {{x}_{1}},{{y}_{1}} \right)$ and B $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.

Note: Remember that if the slope of a line is equal to zero then it is parallel to x-axis and if the slope tends to infinity then it is perpendicular to x-axis. Also, you can remember that if the x-coordinates of the two points through which line passes are same then it must be perpendicular to x-axis and if y-coordinates of the two points through which line passes are same then it must be perpendicular to y-axis or parallel to x-axis.