Question

Prove that the rectangle of maximum area inscribed in a circle is a square.

Answer 1

Hint: In this question we need to prove that the rectangle of maximum area inscribed in a circle is a square. A square has the property that all of its sides are equal. So to prove it assume some sides of the rectangle inscribed within a circle and find out the area. Use the concept of maxima and minima by differentiating the area and then cross verify by taking out the double derivative that it’s a maxima or not. This concept will help in proving the required.

Complete step-by-step answer:

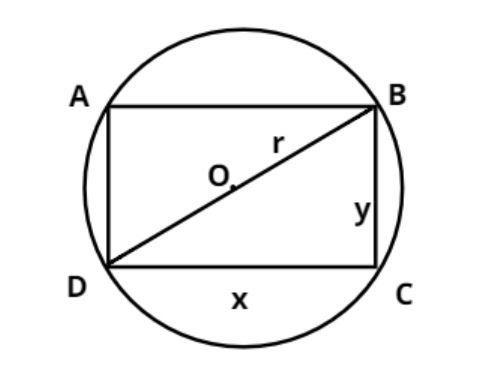
Let ABCD be the rectangle inscribed in the circle with center O and radius (r).
The diagonal of the rectangle will be the diameter of the circle.
As we know diameter (d) is twice the radius.
$\Rightarrow DB = d = 2r$
Since the rectangle has all the four coordinates inscribed on the circumference of the circle.
Hence let the sides of the rectangle be x and y respectively as shown in figure.
Now in triangle BCD apply Pythagoras theorem we have,
$\Rightarrow {\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
$\Rightarrow {\left( {2r} \right)^2} = {x^2} + {y^2}$…………………… (1)
Now the area (A) of the rectangle is length multiplied by breadth.
$\Rightarrow A = xy$………………………. (2)
Now from equation (1) calculate the value of x
$\Rightarrow 4{r^2} = {x^2} + {y^2} \\\ \Rightarrow {x^2} = 4{r^2} - {y^2} \\\$
Now take square root on both sides we have,
$\Rightarrow x = {\left( {4{r^2} - {y^2}} \right)^{\dfrac{1}{2}}}$……………………………….. (3)
Now substitute this value in equation (2) we have,
$\Rightarrow A = y{\left( {4{r^2} - {y^2}} \right)^{\dfrac{1}{2}}}$
Now we have to maximize the area so differentiate the area w.r.t. y and put it equal to zero we have,
$\dfrac{{dA}}{{dy}} = \dfrac{d}{{dy}}\left[ {y{{\left( {4{r^2} - {y^2}} \right)}^{\dfrac{1}{2}}}} \right] = 0$
Here we use product rule of differentiation $\left[ {\dfrac{d}{{dx}}ab = a\dfrac{d}{{dx}}b + b\dfrac{d}{{dx}}a} \right]$ so using this property we have,
$\Rightarrow y\dfrac{d}{{dy}}{\left( {4{r^2} - {y^2}} \right)^{\dfrac{1}{2}}} + {\left( {4{r^2} - {y^2}} \right)^{\dfrac{1}{2}}}\dfrac{d}{{dy}}y = 0$
Now differentiation we have,
$\Rightarrow y\dfrac{{\left( { - 2y} \right)}}{{2{{\left( {4{r^2} - {y^2}} \right)}^{\dfrac{1}{2}}}}} + {\left( {4{r^2} - {y^2}} \right)^{\dfrac{1}{2}}}\left( 1 \right) = 0$
Now simplify the above equation we have,
$\Rightarrow + {\left( {4{r^2} - {y^2}} \right)^{\dfrac{1}{2}}}\left( 1 \right) = y\dfrac{y}{{{{\left( {4{r^2} - {y^2}} \right)}^{\dfrac{1}{2}}}}}$
$\Rightarrow 4{r^2} - {y^2} = {y^2}$
$\Rightarrow 2{y^2} = 4{r^2}$
$\Rightarrow {y^2} = 2{r^2}$
Now take square root on both sides we have,
$\Rightarrow y = r\sqrt 2$
Now substitute this value in equation (3) we have,
$\Rightarrow x = {\left( {4{r^2} - 2{r^2}} \right)^{\dfrac{1}{2}}} = \sqrt {2{r^2}} = r\sqrt 2$
Hence x = y $= r\sqrt 2$ thus it forms a square with maximum area.
So the rectangle of maximum area inscribed in a circle is a square.

Note: Whenever we face such types of problems the key concept is simply to have a diagrammatic representation of the information provided in the question as it helps to understand the basic geometry of the figure. Having a good gist of the properties of rectangle and square helps in getting the answer.