Question

Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.

Answer 1

Hint: First of all, draw the diagram for the problem with the given data which will give us a clear idea of what we have to find. Then find the curved surface area of the cylinder and then prove the problem by using a second derivative test.

Complete step-by-step answer:

Let ${\text{OC}} = r$ be the radius of the cone
${\text{OA}} = h$ be the height of the cone
$\angle {\text{OAQ}} = \alpha$ be the semi vertical angle of the cone
Let ${\text{OE}} = x$ be the radius of the cylinder
${\text{OO'}} =$ height of the cylinder

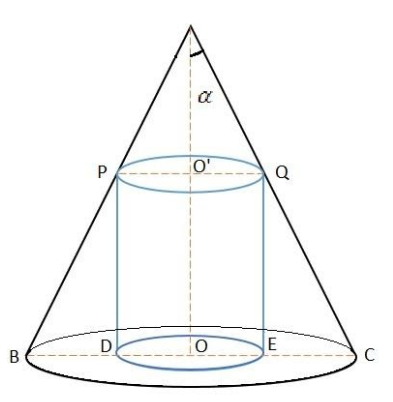
From the diagram,
In $\Delta {\text{AO'Q}}$

$$\tan \alpha = \dfrac{{{\text{O'Q}}}}{{{\text{AO'}}}} \\\ \tan \alpha = \dfrac{{{\text{OE}}}}{{{\text{OA - O'O}}}} \\\ \tan \alpha = \dfrac{x}{{h - {\text{O'O}}}}...........................................\left( 1 \right) \\\$$

In $\Delta {\text{AOC}}$

$$\tan \alpha = \dfrac{{{\text{OC}}}}{{{\text{OA}}}} \\\ \tan \alpha = \dfrac{r}{h}...........................................\left( 2 \right) \\\$$

From equations (1) and (2), we have

$$\dfrac{x}{{h - {\text{O'O}}}} = \dfrac{r}{h} \\\ \dfrac{{hx}}{r} = h - {\text{O'O}} \\\ {\text{O'O}} = \dfrac{{hr - hx}}{r} \\\ {\text{O'O}} = \dfrac{{h\left( {r - x} \right)}}{r} \\\$$

We know that the curved surface of cylinder $= 2\pi \times {\text{Radius}} \times {\text{Height}}$
So, curved surface area of cylinder is given by

$$S = 2\pi \times x \times {\text{O'O}} \\\ S = 2\pi xh\dfrac{{\left( {r - x} \right)}}{r} \\\ S = \dfrac{{2\pi h}}{r}\left( {rx - {x^2}} \right){\text{ }}\left( {{\text{where k}} = \dfrac{{2\pi h}}{r}{\text{ is a constant}}} \right) \\\$$

Now, differentiating S w.r.t $x$ i.e., $S'\left( x \right)$

$$S' = \dfrac{d}{{dx}}\left( {k\left( {rx - {x^2}} \right)} \right) \\\ S' = k\dfrac{d}{{dx}}\left( {rx - {x^2}} \right) \\\ \therefore S' = k\left( {r - 2x} \right) \\\$$

Now, differentiating $S'\left( x \right)$ w.r.t again $x$ i.e., $S''\left( x \right)$

$$S'' = \dfrac{d}{{dx}}\left( {k\left( {r - 2x} \right)} \right) \\\ S'' = k\dfrac{d}{{dx}}\left( {r - 2x} \right) \\\ S'' = k\left( {0 - 2} \right) \\\ \therefore S'' = - 2k \\\$$

We know that the minimum or maximum value of S occurs at $S'\left( x \right) = 0$
So, put $S'\left( x \right) = 0$

$$k\left( {r - 2x} \right) = 0 \\\ \therefore x = \dfrac{r}{2} \\\$$

Now, finding $S''\left( x \right)$ at $x = \dfrac{r}{2}$, we have

$${{S''}_{x = \dfrac{r}{2}}} = - 2k < 0 \\\ \therefore {{S''}_{x = \dfrac{r}{2}}} < 0 \\\$$

Therefore, $x = \dfrac{r}{2}$ is maxima of S.
As the second derivative of the curved surface area of the cylinder is less than zero, the radius of cylinder with greatest curved surface area which can be inscribed in a given cone is half of that cone.

Note: The curved surface area of the cylinder with radius $r$ and height $h$ is given by $S = 2\pi rh$. The second derivative test is used to determine whether a stationary point is a local maximum or a local minimum.