Question

Prove that the points, $A( - 3, - 2),B(5, - 2),C(9,3),D(1,3)$ are the vertices of a parallelogram.

Answer 1

Here we are given 4 points. To prove that it is a parallelogram, we need to calculate the length of the sides, we use the distance formula for it. And then check if opposite sides are equal.

Complete step-by-step answer:
We know that the distance between the two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is,
$d = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;$
Let the given vertices be $A = \left( { - 3, - 2} \right),\;B = \left( {5, - 2} \right),\;C = (9,3)$ and $D = \left( {1,3} \right)$

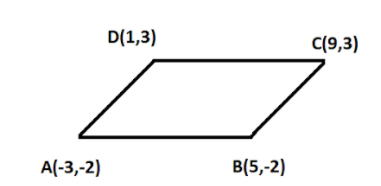
We first find the distance between $A = \left( { - 3, - 2} \right)\;$and $B = \left( {5, - 2} \right)\;\;$as follows:
$AB = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;$​
On substituting the values of $A = \left( { - 3, - 2} \right)\;$and $B = \left( {5, - 2} \right)\;\;$, we get,
$= \sqrt {{{\left( {5 - ( - 3)} \right)}^2} + {{\left( {( - 2) - ( - 2)} \right)}^2}} \;$
On simplifying we get,
$= \sqrt {{{\left( {8} \right)}^2} + {{\left( {0} \right)}^2}} \;$
$= \sqrt {64}$
On taking positive root we get,
$= 8$units
Similarly, the distance between $B = \left( {5, - 2} \right)\;$and $C = \left( {9,3} \right)\;$ is:
$BC = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;$
On substituting the values of $B = \left( {5, - 2} \right)\;$and $C = \left( {9,3} \right)\;$, we get,
$= \sqrt {{{\left( {9 - 5} \right)}^2} + {{\left( {3 - ( - 2)} \right)}^2}} \;$
On simplifying we get,
$= \sqrt {{{\left( 4 \right)}^2} + {{\left( {5} \right)}^2}} \;$
$= \sqrt {16 + 25} \;$
$= \sqrt {41} \;$units
Now, the distance between $C = \left( {9,3} \right)\;$ and $D = (1,3)\;$is:
$CD = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;$
On substituting the value of $C = \left( {9,3} \right)\;$ and $D = (1,3)\;$, we get,
$= \sqrt {{{\left( {1 - 9} \right)}^2} + {{\left( {3 - 3} \right)}^2}} \;$
On further simplification we get,
$= \sqrt {{{\left( { - 8} \right)}^2} + {{\left( 0 \right)}^2}} \;$
$= \sqrt {64} \;$
On taking positive square root we get,
$= 8$units
Now, the distance between $D = \left( {1,3} \right)\;$and $A = \left( { - 3, - 2} \right)\;$ is:
$DA = \sqrt {{{\left( {{x_{2}} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \;$
On substituting the values of $D = \left( {1,3} \right)\;$and $A = \left( { - 3, - 2} \right)\;$, we get,
$= \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( { - 2 - 3} \right)}^2}} \;$
On simplifying further we get,
$= \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 5} \right)}^2}} \;$
$= \sqrt {16 + 25} \;$
$= \sqrt {41}$units
We also know that if the opposite sides have equal side lengths, then ABCD is a parallelogram.
Here, since the lengths of the opposite sides are equal that is:
$AB = CD = 8$units and $BC = DA = \sqrt {41}$units.
Hence, the given vertices are the vertices of a parallelogram.

Note: There are also other important properties of parallelograms to know:
1.Opposite sides are congruent $\left( {AB{\text{ }} = {\text{ }}DC} \right).$
2.Opposite angles are congruent $\left( {D{\text{ }} = {\text{ }}B} \right).$
3.Consecutive angles are supplementary $\left( {A{\text{ }} + {\text{ }}D{\text{ }} = {\text{ }}180^\circ } \right).$
4.If one angle is right, then all angles are right.
5.The diagonals of a parallelogram bisect each other.
6.Each diagonal of a parallelogram separates it into two congruent triangles.