Question

Prove that the points (-3, 0), (1, -3) and (4, 1) are the vertices of an isosceles right-angled triangle. Find the area of this triangle.

Answer 1

To solve this question, we have to remember that in an isosceles triangle two of the three sides are equal and the area of the isosceles triangle is given by $\dfrac{1}{2} \times base \times height$, here we will also use the distance formula, i.e. $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$

Complete step-by-step answer:
Given that,
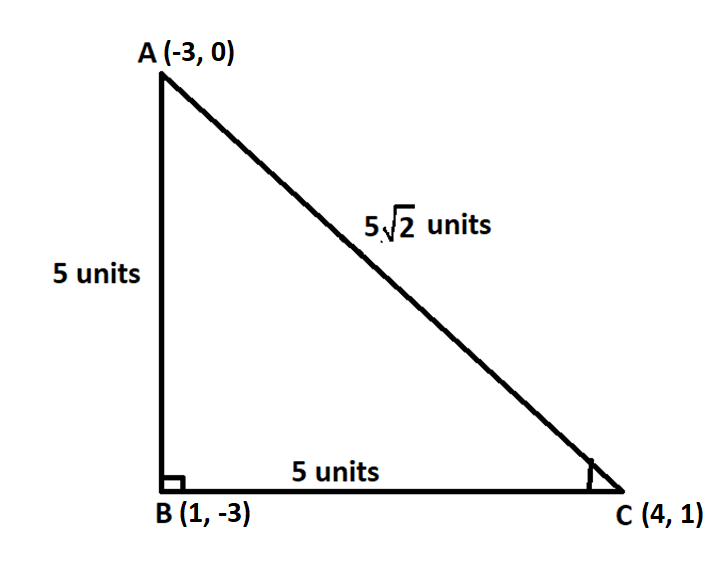
(-3, 0), (1, -3) and (4, 1) are three points.
We have to prove that these are vertices of a right-angled isosceles triangle.
So,
As we know that the distance between two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by
$\Rightarrow d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
Let us say A = (-3, 0), B = (1, -3) and C = (4, 1).
We will find the distance of AB, BC and AC.
So,
$\Rightarrow AB = \sqrt {{{\left( {1 - \left( { - 3} \right)} \right)}^2} + {{\left( { - 3 - 0} \right)}^2}}$
$\Rightarrow AB = \sqrt {{{\left( 4 \right)}^2} + {{\left( { - 3} \right)}^2}}$
$\Rightarrow AB = \sqrt {16 + 9} = \sqrt {25}$
$\Rightarrow AB = 5$ units.
Now,
$\Rightarrow BC = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {1 - \left( { - 3} \right)} \right)}^2}}$
$\Rightarrow BC = \sqrt {{{\left( 3 \right)}^2} + {{\left( 4 \right)}^2}}$
$\Rightarrow BC = \sqrt {9 + 16} = \sqrt {25}$
$\Rightarrow BC = 5$ units.
Also,
$\Rightarrow AC = \sqrt {{{\left( {4 - \left( { - 3} \right)} \right)}^2} + {{\left( {1 - 0} \right)}^2}}$
$\Rightarrow AC = \sqrt {{{\left( 7 \right)}^2} + {{\left( 1 \right)}^2}}$
$\Rightarrow AC = \sqrt {49 + 1} = \sqrt {50}$
$\Rightarrow AC = 5\sqrt 2$ units.
Here, we can see that $AB = BC \ne AC$,
Hence, $\vartriangle ABC$is an isosceles triangle.
Since AB = BC < AC
And it is a right-angled triangle therefore AC should be hypotenuse of the triangle.
So,
We know that
Area of triangle = $\dfrac{1}{2} \times base \times height$ [height = perpendicular]
We have, base = BC = 5 units and perpendicular = AB = 5 units.
$\Rightarrow$ Area of triangle = $\dfrac{1}{2} \times 5 \times 5$
$\Rightarrow$ Area of triangle = $\dfrac{{25}}{2}$ sq. units

Note: In such types of questions always remember the condition of isosceles triangle, the area of right angled triangle and the distance formula between two points which are stated above then using this formula first calculate the distance between the points and check whether it makes a isosceles triangle using the property of isosceles triangle, then calculate the area of the right angle triangle as above, which is the required answer.