Question

Prove that the points (2, -1), (0, 2), (2, 3) and (4, 0) are the coordinates of the vertices of a parallelogram and find the angle between its diagonals.

Answer 1

Hint:Let us name the points as A (2, -1), B (0, 2), C (2, 3) and D (4, 0). Then find the distance between A & B, B & C, C & D, D & A and then compare the lengths of the sides AB, BC, CD & DA. We know from the properties of a parallelogram that opposite sides of a parallelogram are parallel and equal. For finding the angle between its diagonals write the slope of the two diagonals and then using geometry find the angle between the two diagonals.

Complete step-by-step answer:
In the following figure, we have shown a parallelogram ABCD that we have to prove.

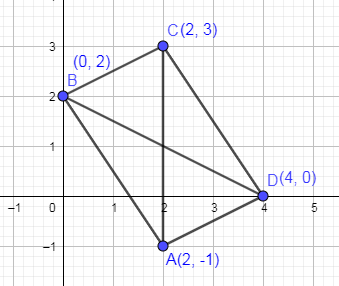
Using the distance formula, we are going to find the distance between A & B, B & C, C & D, D & A.
We know that distance between the two points $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ is equal to:
$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Distance between $A\left( 2,-1 \right)\And B\left( 0,2 \right)$ is:
$\begin{aligned} & \sqrt{{{\left( 0-2 \right)}^{2}}+{{\left( 2+1 \right)}^{2}}} \\\ & =\sqrt{4+9}=\sqrt{13} \\\ \end{aligned}$
Distance between $B\left( 0,2 \right)\And C\left( 2,3 \right)$ is:
$\begin{aligned} & \sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}} \\\ & =\sqrt{4+1}=\sqrt{5} \\\ \end{aligned}$
Distance between $C\left( 2,3 \right)\And D\left( 4,0 \right)$ is:

& \sqrt{{{\left( 4-2 \right)}^{2}}+{{\left( 0-3 \right)}^{2}}} \\\ & =\sqrt{4+9}=\sqrt{13} \\\ \end{aligned}$$ Distance between $D\left( 4,0 \right)\And A\left( 2,-1 \right)$ is: $$\begin{aligned} & \sqrt{{{\left( 2-4 \right)}^{2}}+{{\left( -1-0 \right)}^{2}}} \\\ & =\sqrt{4+1}=\sqrt{5} \\\ \end{aligned}$$ From the above distances, you can see that AB = CD and BC = DA. From the figure that we have drawn above, you can see that AB and CD are the opposite facing sides and they are equal. Similarly, BC and DA are the opposite facing sides and they are equal. This is proving one of the properties of a parallelogram that opposite facing sides are equal. Now, we have to show that the slope of opposite facing sides is equal. The formula for calculating the slope is given by $m=\dfrac{y_2-y_1}{x_2-x_1}$ As AB and CD are sides facing opposite to each other so the slope of AB and CD is: The slope of AB is: ${{m}_{AB}}=\dfrac{2+1}{0-2}=-\dfrac{3}{2}$ The slope of CD is: ${{m}_{CD}}=\dfrac{0-3}{4-2}=-\dfrac{3}{2}$ Hence, the slope of AB and CD are equal. It means AB is parallel to CD. Similarly, we can show that BC and DA are parallel as follows: The slope of BC is: ${{m}_{BC}}=\dfrac{3-2}{2-0}=\dfrac{1}{2}$ The slope of DA is: ${{m}_{DA}}=\dfrac{0+1}{4-2}=\dfrac{1}{2}$ Hence, the slope of BC and DA is equal. It means BC and DA are parallel to each other. The other property of the parallelogram is also satisfied that sides facing opposite to each other are parallel to each other. As, we have proved above that the opposite facing sides are equal and parallel. Hence, we have proved that the points given above are the coordinates of the vertices of a parallelogram. Now, we are going to find the angle between the diagonals AC and BD. Let us assume that ${{m}_{1}}$ is the slope of the diagonal BD and ${{m}_{2}}$ is the slope of the diagonal AC. The slope of the diagonal BD is: ${{m}_{1}}=\dfrac{0-2}{4-0}=-\dfrac{1}{2}$ The slope of the diagonal AC is: ${{m}_{2}}=\dfrac{3+1}{2-2}=\dfrac{4}{0}$ It means slope of AC is not defined or AC is making an angle of 90° from the x – axis. In the below figure, the vertical line is the diagonal AC and BD we have shown by the vertices.  The above figure is the representation of two diagonals according to the slope that we have got. $\theta $is the angle between the two diagonals which we have shown in the above figure. In $\Delta BOD$, OB = 2 and OD = 4 so by trigonometric ratios we can find the angle$\theta $. $\tan \theta =\dfrac{OD}{OB}=\dfrac{4}{2}=2$ Hence, the angle between the diagonals is ${{\tan }^{-1}}\left( 2 \right)$. Note: You might think of finding the angle between the two diagonals by using the formula, $\tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$ But one of the slopes of the diagonals is not defined so we cannot use the formula and we have found the angles between the diagonals using geometry.