Question

Prove that the parabola ${{y}^{2}}=16x$ and the circle ${{x}^{2}}+{{y}^{2}}-40x-16y-48=0$ meet at the point $P(36,24)$ and one other point Q, find that point. Prove that $PQ$ is a diameter of the circle.

Answer 1

Hint: To find the points of intersection of the parabola and the circle, we will substitute the equation of the parabola in the equation of the circle .Solve the equations to get the desired points. Use distance formula to calculate the distance between points P and Q to prove that the distance PQ is equal to the length of diameter of the circle.

Complete step by step answer: -
We have a parabola ${{y}^{2}}=16x$ and a circle ${{x}^{2}}+{{y}^{2}}-40x-16y-48=0$ which intersect at points $P(36,24)$ and Q. We have to find another point of intersection of two curves.

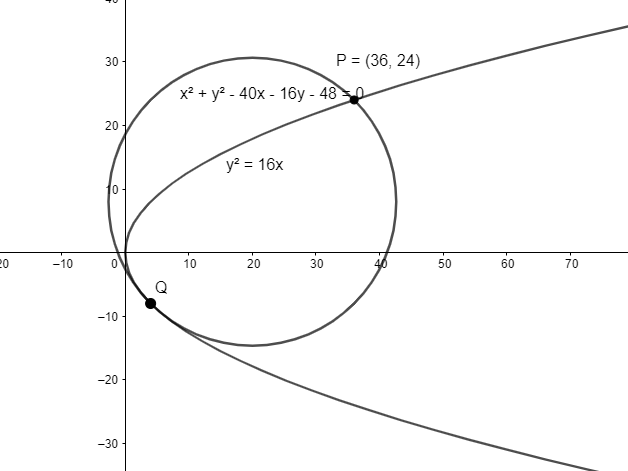
To find the point of intersection of the two curves, we will substitute the equation of parabola into the equation of the circle.
We can rewrite the equation ${{y}^{2}}=16x$ by taking the square root on both sides as $y=\pm 4\sqrt{x}$.
Firstly, we will consider $y=4\sqrt{x}$.
Substituting this in the equation of the circle, we get ${{x}^{2}}+16x-40x-16\times 4\sqrt{x}-48=0$.
Let’s assume $\sqrt{x}=a.....\left( 1 \right)$.
Thus, our new equation is ${{a}^{4}}-24{{a}^{2}}-64a-48=0$.
We will now factorize the above equation by adding and subtracting$6{{a}^{3}}$.

& \Rightarrow {{a}^{4}}-24{{a}^{2}}-64a-48={{a}^{4}}-6{{a}^{3}}+6{{a}^{3}}-24{{a}^{2}}-64a-48=0 \\\ & \Rightarrow {{a}^{4}}-6{{a}^{3}}+6{{a}^{3}}-24{{a}^{2}}-64a-48=0 \\\ & \Rightarrow {{a}^{3}}(a-6)+6{{a}^{3}}-36{{a}^{2}}+12{{a}^{2}}-64a-48=0 \\\ & \Rightarrow {{a}^{3}}(a-6)+6{{a}^{2}}(a-6)+4(3{{a}^{2}}-16a-12)=0 \\\ & \Rightarrow {{a}^{3}}(a-6)+6{{a}^{2}}(a-6)+4(3{{a}^{2}}-18a+2a-12)=0 \\\ & \Rightarrow {{a}^{3}}(a-6)+6{{a}^{2}}(a-6)+4\\{3a(a-6)+2(a-6)\\}=0 \\\ & \Rightarrow {{a}^{3}}(a-6)+6{{a}^{2}}(a-6)+4(a-6)(3a+2)=0 \\\ & \Rightarrow (a-6)({{a}^{3}}+6{{a}^{2}}+12a+8)=0 \\\ & \Rightarrow (a-6)({{a}^{3}}+4{{a}^{2}}+2{{a}^{2}}+12a+8)=0 \\\ & \Rightarrow (a-6)({{a}^{2}}(a+2)+4({{a}^{2}}+3a+2))=0 \\\ & \Rightarrow (a-6)({{a}^{2}}(a+2)+4(a+1)(a+2))=0 \\\ & \Rightarrow (a-6)(a+2)({{a}^{2}}+4a+4)=0 \\\ & \Rightarrow (a-6)(a+2){{(a+2)}^{2}}=0 \\\ & \Rightarrow (a-6){{(a+2)}^{3}}=0 \\\ \end{aligned}$$ So, we get $${{(a+2)}^{3}}(a-6)=0$$. Thus, we have $$a=-2,6$$. Substituting $$a=6$$ in the equation $$(1)$$, we have $$x=36$$. Substituting $$x=36$$ in the equation of parabola $${{y}^{2}}=16x$$, we have ${{y}^{2}}=16\times 36$. Thus, we have $y=\sqrt{16\times 36}=\pm 24$. Substituting $$x=36$$ in the equation of circle $${{x}^{2}}+{{y}^{2}}-40x-16y-48=0$$, we have ${{\left( 36 \right)}^{2}}+{{y}^{2}}-40\left( 36 \right)-16y-48=0$. Thus, we have ${{y}^{2}}-16y=48+1440-1296=192$. We will now factorize the equation ${{y}^{2}}-16y=192$ by splitting the middle term. We can rewrite the previous equation as ${{y}^{2}}-24y+8y-192=0$. Taking out the common terms, we have $y\left( y-24 \right)+8\left( y-24 \right)=0$. So, we have $\left( y-24 \right)\left( y+8 \right)=0$. Thus, we have $y=24,-8$. For parabola, we have $y=\sqrt{16\times 36}=\pm 24$ and for the circle, we have $y=24,-8$. So, the value of y which satisfies both circle and parabola is $y=24$. Thus $$P(36,24)$$ is one of the points of intersection of two curves. Now, we will find other points of intersection using $$a=-2$$. Substituting $$a=-2$$ in the equation $$(1)$$, we get $$x=4$$. Substituting $$x=4$$ in the equation of parabola $${{y}^{2}}=16x$$, we have ${{y}^{2}}=16\times 4$. Thus, we have $y=\sqrt{16\times 4}=\pm 8$. Substituting $$x=4$$ in the equation of circle $${{x}^{2}}+{{y}^{2}}-40x-16y-48=0$$, we have ${{\left( 4 \right)}^{2}}+{{y}^{2}}-40\left( 4 \right)-16y-48=0$. Thus, we have ${{y}^{2}}-16y=48+160-16=192$. We will now factorize the equation ${{y}^{2}}-16y=192$ by splitting the middle term. We can rewrite the previous equation as ${{y}^{2}}-24y+8y-192=0$. Taking out the common terms, we have $y\left( y-24 \right)+8\left( y-24 \right)=0$. So, we have $\left( y-24 \right)\left( y+8 \right)=0$. Thus, we have $y=24,-8$. For parabola, we have $y=\sqrt{16\times 4}=\pm 8$ and for the circle, we have $y=24,-8$. So, the value of y which satisfies both circle and parabola is $y=-8$. Thus the other point of intersection of the two curves is (4, -8). So, we have $$Q=(4,-8)$$. Now to prove that $$PQ$$ is the diameter of the circle, we will find distance between the two points. We know that distance between two points of the form $$({{x}_{1}},{{y}_{1}})$$ and $$({{x}_{2}},{{y}_{2}})$$ is $$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$$. Substituting $${{x}_{1}}=36,{{y}_{1}}=24,{{x}_{2}}=4,{{y}_{2}}=-8$$, we get $$PQ=\sqrt{{{(36-4)}^{2}}+{{(24+8)}^{2}}}=\sqrt{{{32}^{2}}+{{32}^{2}}}=32\sqrt{2}$$ units. We know that the circle of the form $${{x}^{2}}+{{y}^{2}}-2gx-2hy+c=0$$ has radius $$\sqrt{{{g}^{2}}+{{h}^{2}}-c}$$ units. Substituting $$g=20,h=8,c=48$$, we get radius $$=\sqrt{{{20}^{2}}+{{8}^{2}}+48}=16\sqrt{2}$$ units. As, diameter of the circle $$=2\times $$ radius, we have diameter $$=2\times 16\sqrt{2}=32\sqrt{2}$$ units. We observe that the length of PQ is equal to the diameter of the circle. Hence, PQ is the diameter of the circle. Note: We can also solve this question by substituting the equation of circle in the equation of parabola and then solving it to get the point of intersection of two curves. It’s necessary to use the distance formula to prove that PQ is the diameter of the circle.