Question

Prove that the orthocentres of the triangles formed by three tangents and the corresponding three normals to a parabola are equidistant from the axis.

Answer 1

There are three points on the parabola where we are trying to find the tangents and normal. So, we use the formula of the equation of tangents for general equations to find the intersecting points. After getting those points with the help of the slope of normal we find intersecting points for normal. These points create the point for the orthocentre which is equidistant from the axes.

Complete step-by-step solution:
Let the parabola be ${{y}^{2}}=4ax$ …(i)
Now, let the points $\left( a{{t}_{1}}^{2},-2a{{t}_{1}} \right),\left( a{{t}_{2}}^{2},-2a{{t}_{2}} \right),\left( a{{t}_{3}}^{2},-2a{{t}_{3}} \right)$ be the coordinates of points P, Q, R respectively.
The orthocentre of a triangle is the intersecting point of the altitudes of that triangle.
We are trying to find the tangents and the normal of the parabola on those three points.
The general equation of tangent of parabola ${{y}^{2}}=4ax$is $-y{{t}_{i}}=x+{{x}_{i}}$ where $\left( {{x}_{i}},{{y}_{i}} \right)=\left( a{{t}_{i}}^{2},2a{{t}_{i}} \right)$.
Here the value of “i” runs from 1 to 3. So, $i=1(1)3$.
Then, the equation of the tangents at P, Q and R with respect to the parabola (i) are $-y{{t}_{1}}=x+{{x}_{1}}=x+a{{t}_{1}}^{2}$ ……………...…(ii)
$-y{{t}_{2}}=x+{{x}_{2}}=x+a{{t}_{2}}^{2}$ ……………...…(iii)
$-y{{t}_{3}}=x+{{x}_{3}}=x+a{{t}_{3}}^{2}$ ……………...…(iv)
Solving (ii) and (iii) we have the coordinates of the points of the points of intersection say A as
$-y{{t}_{1}}=x+a{{t}_{1}}^{2}\Rightarrow -y=\dfrac{x+a{{t}_{1}}^{2}}{{{t}_{1}}}$ and $-y{{t}_{2}}=x+a{{t}_{2}}^{2}\Rightarrow -y=\dfrac{x+a{{t}_{2}}^{2}}{{{t}_{2}}}$.
So, the intersection is $\dfrac{x+a{{t}_{1}}^{2}}{{{t}_{1}}}=\dfrac{x+a{{t}_{2}}^{2}}{{{t}_{2}}}\Rightarrow x=a{{t}_{1}}{{t}_{2}}$ and $-y=\dfrac{a{{t}_{1}}{{t}_{2}}+a{{t}_{1}}^{2}}{{{t}_{1}}}\Rightarrow y=-a\left( {{t}_{1}}+{{t}_{2}} \right)$.
Now equation to the line through A and perpendicular to (iii) will be $y+a\left( {{t}_{1}}+{{t}_{2}} \right)={{t}_{3}}\left( a{{t}_{1}}{{t}_{3}} \right)$ …(v)
Similarly, the equation to the line through B, the point of intersection of (iii) and (iv) and perpendicular to (ii) is $y+a\left( {{t}_{2}}+{{t}_{3}} \right)={{t}_{1}}\left( x-a{{t}_{2}}{{t}_{3}} \right)$ …(vi)
On solving (v) and (vi) we get the ordinate of the triangle formed by (ii), (iii) and (iv) as $-a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{1}}{{t}_{2}}{{t}_{3}} \right)$
Again, equation to the normal at P, Q & R are respectively
$y={{t}_{1}}x-2a{{t}_{1}}-a{{t}_{1}}^{3}$ ……………..…(vii)
$y={{t}_{2}}x-2a{{t}_{2}}-a{{t}_{2}}^{3}$ ……………..…(viii)
$y={{t}_{3}}x-2a{{t}_{3}}-a{{t}_{3}}^{3}$ ……………….…(ix)
On solving (vii) and (viii) we get the coordinate of one of the vertices of the triangle formed by these three normal as $2a+a\left( {{t}_{1}}^{2}+{{t}_{2}}^{2}+{{t}_{1}}{{t}_{2}} \right),a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right)$.
Equation to the line through this point and perpendicular to (ix) is
$y-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right)=-\dfrac{1}{{{t}_{2}}}\left( x-2a-a{{t}_{1}}^{2}-a{{t}_{2}}^{2}-a{{t}_{1}}{{t}_{2}} \right)$ …(x)
Similarly, the equation to the other perpendicular will be
$y-a{{t}_{2}}{{t}_{3}}\left( {{t}_{2}}+{{t}_{3}} \right)=-\dfrac{1}{{{t}_{1}}}\left( x-2a-a{{t}_{2}}^{2}-a{{t}_{3}}^{2}-a{{t}_{2}}{{t}_{3}} \right)$ ……...…(xi)

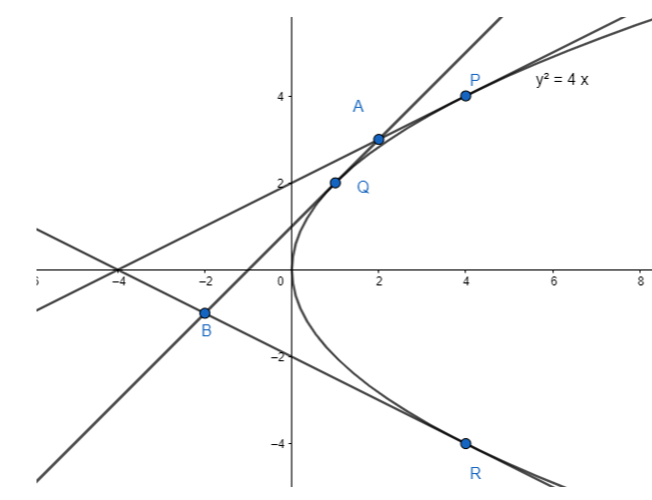
On solving (x) and (xi) we get the ordinate of the point of intersection as $-a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{1}}{{t}_{2}}{{t}_{3}} \right)$.
This is also the ordinate of the point of intersection or orthocentre of the triangle formed by tangents.
Hence the ortho centers are equidistant from the axis that is the x-axis.

Note: We can use theorem of normal to use directly. At the time of finding of intersecting points we also need to elaborate that part. Instead of taking the general equation ${{\left( y-p \right)}^{2}}=4a\left( x-q \right)$ where $\left( p,q \right)$ is the vertex we took ${{y}^{2}}=4ax$. This makes the problem easier as the vertex is irrelevant in finding the distance.