Question
Question: Prove that, the normal to \({{y}^{2}}=12x\) at \(\left( 3,6 \right)\) meets the parabola again in \(...
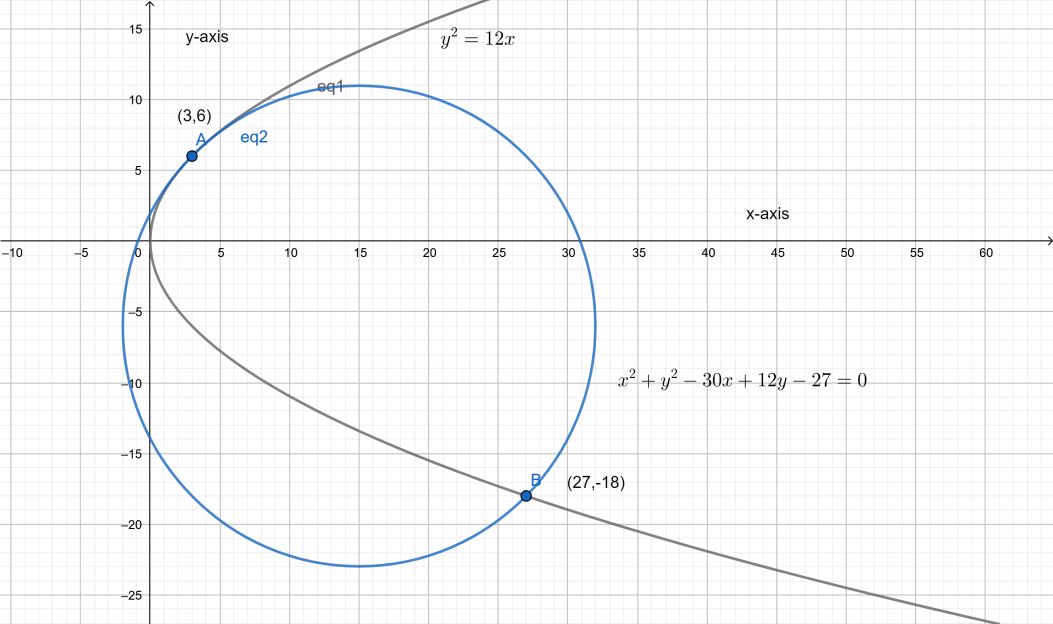
Prove that, the normal to y2=12x at (3,6) meets the parabola again in (27,−18) and circle on this normal chord as diameter is x2+y2−30x+12y−27=0.
Solution
From the question given that we have to prove that, the normal to y2=12x at (3,6) meets the parabola again in (27,−18) and circle on this normal chord as diameter is x2+y2−30x+12y−27=0. As we know that the general equation of a parabola is y2=4ax and the general point is (at2,2at), and the general equation of the normal for this parabola is y+tx=2at+at3.
Complete step-by-step answer:
From the above question the given parabola is
⇒y2=12x
Now we will rearrange the given parabola as
⇒y2=4×3×x
As we know that the general equation of a parabola is
⇒y2=4ax
Now compare this with the given parabola equation, we will get,
⇒y2=4×3×x=4ax
⇒a=3
and the general point is
⇒(at2,2at)
Now we will compare (3,6) with the general point of parabola,
⇒(at2,2at)=(3,6)
From this we will get,
⇒2at=6
⇒2×3×t=6
⇒t=1
As we know that the general equation of normal to the parabola is
⇒y+tx=2at+at3
Now we have to substitute the values in their respective position we will get,
⇒y+x=6+3
⇒y+x=9
⇒y=9−x
From the question given that the parabola intersects again with this normal,
⇒y2=12x
In place of y, we will substitute the intersection point y=9−x
⇒(9−x)2=12x
⇒81−18x+x2=12x
⇒x2−30x+81=0
By further simplification we will get,
⇒x2−27x−3x+81=0
⇒x(x−27)−3(x−27)=0
⇒(x−27)(x−3)=0
⇒x=3,27
x=3is already taken as point of normal and general point of parabola,
So,x=27 then
⇒y=9−x
⇒y=9−27
⇒y=−18
Hence the parabola meets normal at (27,−18)
Given that this normal chord as diameter then centre of the circle will be the midpoint of these two intersection of normal points with the parabola,
Therefore, the centre is
⇒centre=(23+27,26−18)
⇒centre=(15,−6)
Now the radius of the circle will be the distance from the centre to any of the intersection points, we will find the distance between the centre and the point (3,6) this distance will be the radius.
⇒radius=(15−3)2+(−6−6)2
⇒radius=(12)2+(12)2
⇒radius=122
As we know that the general equation of circle having centre (h,k) and radius r is
⇒(x−h)2+(y−k)2=r2
From this the required circle equation is
⇒(x−15)2+(y−(−6))2=(122)2
By further simplification we will get,
⇒x2−30x+225+y2+12y+36=288
⇒x2+y2−30x+12y−27=0
Therefore, hence proved.
The graph of this would be as follows.
Note: Students should recall all the general equations formulas of parabola and circle before doing this problem. Students should also know that the general equation of parabola having centre (h,k) is
⇒(y−k)2=4a(x−h) . students should be careful while doing the calculations.
