Solveeit Logo
Login

Question

Question: Prove that the normal to \({{y}^{2}}=12x\) at ( 3, 6 ) meets the parabola again in ( 27, -18 ) and c...

Prove that the normal to y2=12x{{y}^{2}}=12x at ( 3, 6 ) meets the parabola again in ( 27, -18 ) and circle on this normal chord as diameter is x2+y2−30x+12y−27=0{{x}^{2}}+{{y}^{2}}-30x+12y-27=0

Explanation

Solution

Hint: First we will write the equation of normal (y−y1)=−y12a(x−x1)\left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right) and then we use that equation and will put that value in the equation of parabola to find the other point and then using these two points as diameter we will find the equation of circle.

Complete step-by-step solution -


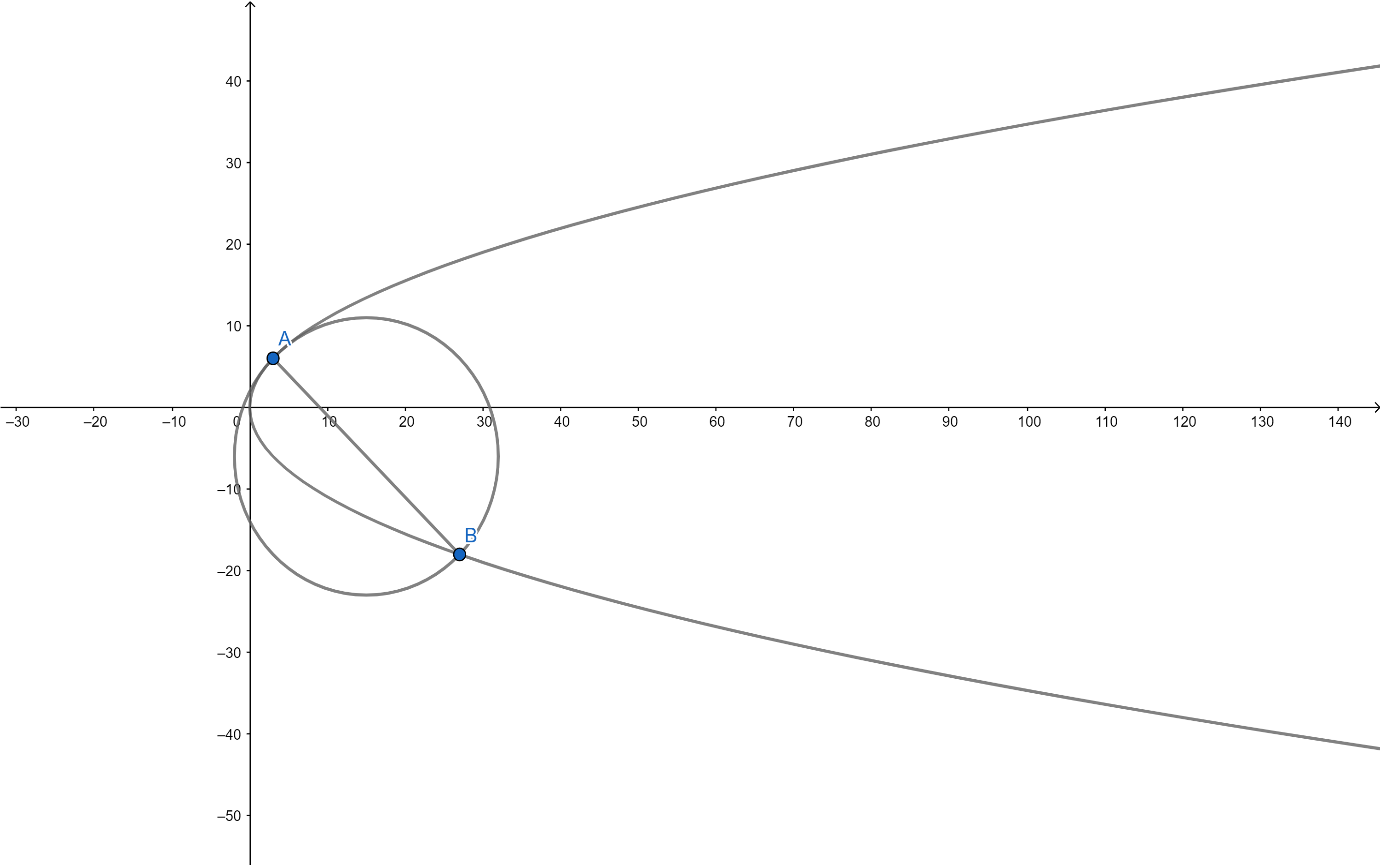
Here A and B are the two given points.
If the equation of parabola is y2=4ax{{y}^{2}}=4ax then the equation of normal passing through the point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) on the parabola is:
(y−y1)=−y12a(x−x1)\left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right)
Now comparing the values with the question we get,
y1=6 x1=3 a=3 \begin{aligned} & {{y}_{1}}=6 \\\ & {{x}_{1}}=3 \\\ & a=3 \\\ \end{aligned}
Now with using that the equation becomes,
(y−6)=−62×3(x−3) y−6=−x+3 x+y=9 \begin{aligned} & \left( y-6 \right)=\dfrac{-6}{2\times 3}\left( x-3 \right) \\\ & y-6=-x+3 \\\ & x+y=9 \\\ \end{aligned}
Now putting the value of x from this in y2=12x{{y}^{2}}=12x we get,
y2=12(9−y) y2+12y−108=0 \begin{aligned} & {{y}^{2}}=12\left( 9-y \right) \\\ & {{y}^{2}}+12y-108=0 \\\ \end{aligned}
Now we will put y = -18 and if it satisfies then the it meets the parabola again in ( 27, -18 ).

& {{\left( -18 \right)}^{2}}+12\left( -18 \right)-108 \\\ & =324-324 \\\ & =0 \\\ \end{aligned}$$ Hence it satisfies so we have proved it meets the parabola again in ( 27, -18 ). Now the equation of circle if $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the diametric points is: $\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$ Now the two points are (3,6) and (27,-18), The equation of circle is: $\begin{aligned} & \left( x-3 \right)\left( x-27 \right)+\left( y-6 \right)\left( y-\left( -18 \right) \right)=0 \\\ & {{x}^{2}}-27x-3x+27\times 3+{{y}^{2}}+18y-6y-6\times 18=0 \\\ & {{x}^{2}}+{{y}^{2}}-30x+12y-27=0 \\\ \end{aligned}$ Hence, proved. Note: In this question we have used some formulas of finding the normal of parabola, finding the equation of circle with two diametric points are given. So, all of these formulas must be kept in mind while solving this question and one should try to derive it for better understanding.