Question

Prove that the locus of the pole, with respect to the ellipse, of any tangent to the auxiliary circle is the curve
$\dfrac{{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{a}^{2}}}$

Answer 1

Equation of polar w.r.t pole $\left( {{x}_{1}},{{y}_{1}} \right)$ for ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is given as $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$Perpendicular distance of a point $\left( {{x}_{1}},{{y}_{1}} \right)$ from a line Ax + By + C = 0 can be given as
$\Rightarrow \left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$

Complete step-by-step answer:
Consider ellipse equation as $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Let the pole be P (h, k) inside ellipse and polar is line L as shown in diagram

As we know that polar is the line w.r.t pole in ellipse in a way like: - There are infinite number of lines that can be drawn through a pole and each can be termed as chord and cut at two points to ellipse. Tangents (two) can be drawn through each chord and ellipse intersection point as shown below: -

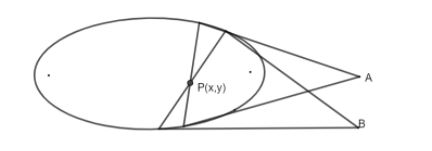
Line joining the points A and B will be termed as polar i.e. all the points we get after drawing two tangents w.r.t P (pole) will lie on a line which is called polar and the equation of that line is T=0.
i.e. $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1$
Now, coming to the question
Equation of ellipse = $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$
Pole assumed= P (h, k)
Pole w.r.t pole
T=0
$\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1$
Hence, equation of polar w.r.t pole P (h, k) is
$\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}=1-(1)$
As it is given that polar given here is tangent to the auxiliary circle. Auxiliary circle is drawn concentric with an ellipse and radius is half of the major axis as shown in the diagram.

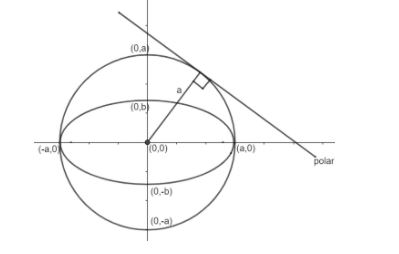
Now, we can observe that the radius ‘a’ shown in figure will be perpendicular to tangent (polar for ellipse).
Hence, the perpendicular distance of polar to centre is a radius.
As we know the formula for calculating perpendicular distance of any line $Ax+By+C=0$from any point $\left( {{x}_{1}},{{y}_{1}} \right)$is
$\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$
Since, Radius of circle = Perpendicular distance of polar to centre.
We have equation of polar is $\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}-1=0$
Comparing above equation with $Ax+By+C=0$we get,
$A=\dfrac{h}{{{a}^{2}}},B=\dfrac{k}{{{a}^{2}}},C=-1$
Hence, Radius of circle = Perpendicular distance of polar to centre.
$a=\left| \dfrac{0+0-1}{\sqrt{{{\left( \dfrac{h}{{{a}^{2}}} \right)}^{2}}+{{\left( \dfrac{k}{{{b}^{2}}} \right)}^{2}}}} \right|$
$a=\left| \dfrac{-1}{\sqrt{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}} \right|$
Squaring both the sides of above equations, we get
${{a}^{2}}=\dfrac{1}{\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}}$
$\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{a}^{2}}}$
Replacing (h, k) to (x, y) required locus: - $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{a}^{2}}}$

Note: Auxiliary circle for any ellipse is radius $=\dfrac{major\ axis}{2}$and concentric with ellipse. Term auxiliary circle should be clear for this question and how to write its equation as well. Take care of mod sign while writing the perpendicular distance in solution.
Another approach would be that we can suppose point of contact of polar to circle as parametric coordinates as $\left( a\cos \theta ,a\sin \theta \right)$and write the tangent equation as T=0 or $x\cos \theta +y\sin \theta =a$and compare it with the polar equation w.r.t (h, k) $\dfrac{hx}{{{a}^{2}}}+\dfrac{ky}{{{b}^{2}}}-1=0$as both represents the same line. And eliminate $\theta$by equating the ratios of the terms of the equations.