Question

Prove that the locus of the middle points of the portions of tangents included between the axes is the curve $\dfrac{{{a}^{2}}}{{{x}^{2}}}+\dfrac{{{b}^{2}}}{{{y}^{2}}}=4$.

Answer 1

To solve this question what we will do is, we will substitute the point of parabola in the equation of tangents then we will replace the ( x, y ) by ( h, k ) and find the value of midpoint of line AB in terms of cosine and sine. And, then we will use identity to find the locus of the middle points of the portions of tangents included between the axes .

Complete step by step solution:

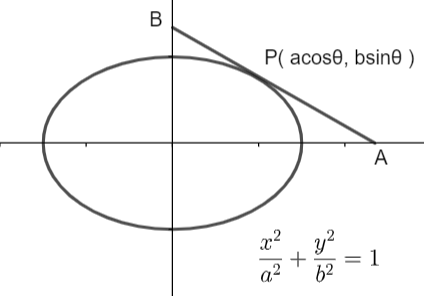
We know that equation of ellipse is $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$. Now. Let AB be tangent on ellipse $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and the point at which curve $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and tangent AB meet be $P(a\cos \theta ,b\sin \theta )$ that is point $P(a\cos \theta ,b\sin \theta )$ lies on both tangent and curve $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
Now, equation of tangent will be equal to, $\dfrac{x\cdot {{x}_{1}}}{{{a}^{2}}}+\dfrac{y\cdot {{y}_{1}}}{{{b}^{2}}}=1$ at point $P(a\cos \theta ,b\sin \theta )$, where $({{x}_{1}},{{y}_{1}})$ are any point on tangent line.
Substituting point $P(a\cos \theta ,b\sin \theta )$ in $\dfrac{x\cdot {{x}_{1}}}{{{a}^{2}}}+\dfrac{y\cdot {{y}_{1}}}{{{b}^{2}}}=1$ to get equation of tangent, we get
$\dfrac{x\cdot (acos\theta )}{{{a}^{2}}}+\dfrac{y\cdot (b\sin \theta )}{{{b}^{2}}}=1$
At, point A, y = 0
So, $\dfrac{x\cdot (cos\theta )}{a}=1$
Or, $x=\dfrac{a}{\cos \theta }$
So, coordinate of A is equals to, $\left( \dfrac{a}{\cos \theta },0 \right)$
Similarly, At, point B, x = 0
So, $\dfrac{y\cdot (sin\theta )}{b}=1$
Or, $y=\dfrac{b}{\sin \theta }$
So, coordinate of A is equals to, $\left( 0,\dfrac{b}{\sin \theta } \right)$
Now, let M be the mid point of line AB, using midpoint formula $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ ,
Coordinates of M will be $\left( \dfrac{\dfrac{a}{\cos \theta }+0}{2},\dfrac{0+\dfrac{b}{\sin \theta }}{2} \right)$
So, M$\left( \dfrac{a}{2\cos \theta },\dfrac{b}{2\sin \theta } \right)$= ( h, k )
So, h = $\dfrac{a}{2\cos \theta }$and k = $\dfrac{b}{2\sin \theta }$
Finding value of $\cos \theta$ and $\sin \theta$ , we get
$\cos \theta =\dfrac{a}{2h}$ and $\sin \theta =\dfrac{b}{2k}$
We know that, ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$
Putting values of $\cos \theta$ and $\sin \theta$ in ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$, we get
${{\left( \dfrac{a}{2h} \right)}^{2}}+{{\left( \dfrac{b}{2k} \right)}^{2}}=1$
On simplifying, we get
$\dfrac{1}{4}\left( {{\left( \dfrac{a}{h} \right)}^{2}}+{{\left( \dfrac{b}{k} \right)}^{2}} \right)=1$
${{\left( \dfrac{a}{h} \right)}^{2}}+{{\left( \dfrac{b}{k} \right)}^{2}}=4$
Replacing, locus points ( h, k ) by ( x, y ) we get
${{\left( \dfrac{a}{x} \right)}^{2}}+{{\left( \dfrac{b}{y} \right)}^{2}}=4$
Hence, the locus of the middle points of the portions of tangents included between the axes is the curve $\dfrac{{{a}^{2}}}{{{x}^{2}}}+\dfrac{{{b}^{2}}}{{{y}^{2}}}=4$.

Note: While solving this question do not confuse between the equation of ellipse. $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ and equation tangent $\dfrac{x\cdot {{x}_{1}}}{{{a}^{2}}}+\dfrac{y\cdot {{y}_{1}}}{{{b}^{2}}}=1$ as here $({{x}_{1}},{{y}_{1}})$ are any point on tangent line.
Calculation must be accurate and avoid making mistakes as this may give incorrect answers.