Question

Prove that the locus of the middle point of a portion of a normal intersected between the curve and the axis is a parabola whose vertex is the focus and whose latus rectum is one quarter of the original parabola.

Answer 1

Hint: The equation of normal in parametric form is given as $y=-tx+2at+a{{t}^{3}}$, where the normal is drawn at a point $P$ with parameter $t$.

First of all , let’s take the equation of the parabola to be ${{y}^{2}}=4ax$.

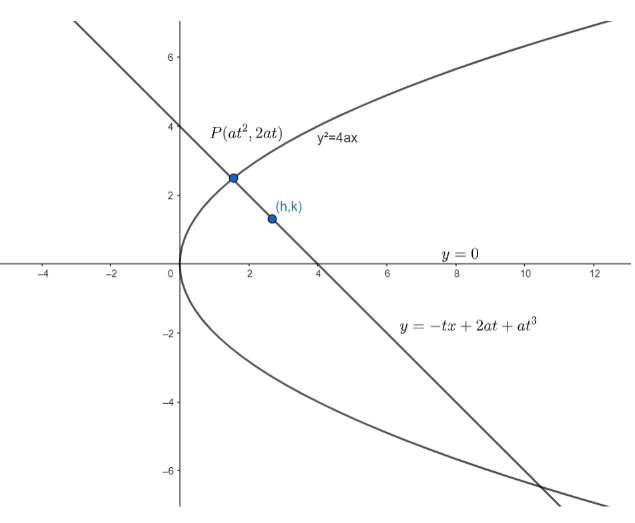
Coordinates of any point on the parabola in parametric form is given as $P\left( a{{t}^{2}},2at \right)$.
We know, equation of normal in parametric form , where the normal is drawn at a point $P$ with parameter $t$, is given as
$y=-tx+2at+a{{t}^{3}}....\left( i \right)$
Also, the equation of axis of the parabola is
$y=0.....\left( ii \right)$
To find the points of intersection of $\left( i \right)$and$\left( ii \right)$, we substitute $y=0$ in $\left( i \right)$.
So, $0=-tx+2at+{{t}^{3}}$
$\Rightarrow x=2a+a{{t}^{2}}$
So , the point of intersection of the axis and the normal is $\left( 2a+a{{t}^{2}},0 \right)$.
Now , let the midpoint of intercepted portion be $\left( h,k \right).....\left( iii \right)$
But we also know that the extremities of the intercepted portion are $\left( a{{t}^{2}},2at \right)$ and $\left( 2a+a{{t}^{2}},0 \right)$.
Now, we know that the coordinates of the midpoint of the line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as: $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
So, the coordinates of the midpoint are
$\left( \dfrac{a{{t}^{2}}+2a+a{{t}^{2}}}{2},\dfrac{2at+0}{2} \right)$
$=\left( a{{t}^{2}}+a,at \right)...\left( iv \right)$
So, from $\left( iii \right)$and $\left( iv \right)$, we can say
$h=a{{t}^{2}}+a....\left( v \right)$, $k=at$
Now, k=at$$$$\Rightarrow t=\dfrac{k}{a}...\left( vi \right)
Substituting $t=\dfrac{k}{a}$in $\left( v \right)$, we get
$h=a{{\left( \dfrac{k}{a} \right)}^{2}}+a$
$\Rightarrow h=\dfrac{{{k}^{2}}}{a}+a$
$\Rightarrow {{k}^{2}}=ah-{{a}^{2}}........$ equation$(vii)$
Now , to get the equation of the locus of $\left( h,k \right)$, we will substitute $(x,y)$ in place of $\left( h,k \right)$ in equation$(vii)$.
Or, ${{y}^{2}}=a\left( x-a \right)....\left( viii \right)$ is the equation of the locus.
Now , we know the length of the latus rectum of ${{y}^{2}}=4ax$ is $4a$.
Now , the length of latus rectum of parabola given by equation $\left( vii \right)$is $4\times \dfrac{a}{4}=a$
Also, the vertex of $\left( viii \right)$ is $\left( a,0 \right)$ which is the focus of ${{y}^{2}}=4ax$
Hence , the length of the latus rectum of the locus is one quarter of the original parabola and the vertex of the locus is the focus of the original parabola .

Note: Length of latus rectum of parabola ${{y}^{2}}=4ax$ is equal to $4a$ and not $a$.
Focus of parabola ${{y}^{2}}=4ax$ is $\left( a,0 \right)$ and not $(4a,0)$.
Students generally get confused and make mistakes which results in wrong answers. So , such mistakes should be avoided .