Question

Prove that the locus of the mid-points of the chord of a parabola passes through the vertex is a parabola.

Answer 1

Hint: Take any general point on the parabola and find the mid-point of the chord with the end points being the vertex and one point on the parabola. Solve the equations to eliminate the parameters and get the locus of mid-point of chord of the parabola which passes through the vertex of the parabola.

Complete step-by-step answer:

Consider a parabola ${{y}^{2}}=4ax$. We want to prove that the middle point of chord of the parabola which passes through the vertex is a parabola.

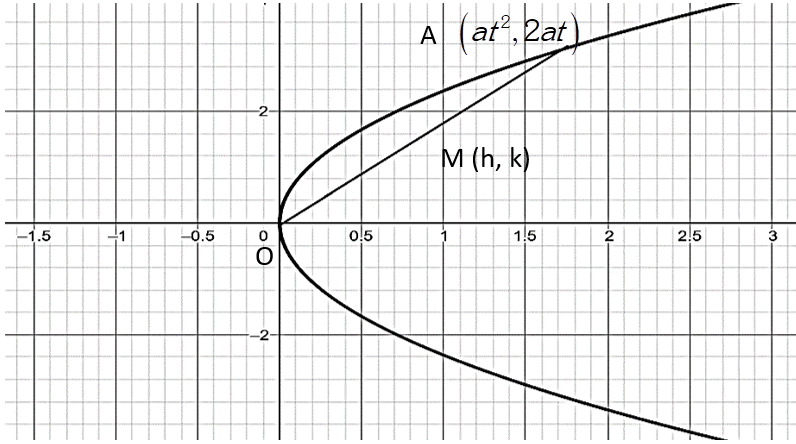
We know that the vertex of the parabola of the form ${{y}^{2}}=4ax$ is $O\left( 0,0 \right)$.
Let us consider any point on the parabola${{y}^{2}}=4ax$ of the form to be $A\left( a{{t}^{2}},2at \right)$.
Let us consider an arbitrary chord $OA$ of the parabola which passes through the vertex $O\left( 0,0 \right)$ and $A\left( a{{t}^{2}},2at \right)$ of the parabola.

We want to find the mid-point of this chord of the parabola.

We know that the mid-point of any two points of the form $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.

Substituting ${{x}_{1}}=0,{{y}_{1}}=0,{{x}_{2}}=a{{t}^{2}},{{y}_{2}}=2at$ in the above equation, we get $\left( \dfrac{0+a{{t}^{2}}}{2},\dfrac{0+2at}{2} \right)$ as the mid-point of the chord joining the points $O\left( 0,0 \right)$ and $A\left( a{{t}^{2}},2at \right)$.

Let’s assume that the locus of mid-point of any chord of the parabola passing through vertex is of the form $\left( x,y \right)$.
Thus, we have $\left( x,y \right)=\left( \dfrac{0+a{{t}^{2}}}{2},\dfrac{0+2at}{2} \right)$.

Comparing the terms, we get $x=\dfrac{a{{t}^{2}}}{2},y=at$.

Rearranging the terms in both equations in terms of the parameter $t$, we get $\dfrac{2x}{a}={{t}^{2}},\dfrac{y}{a}=t$.

Substituting one equation to the other one, we get $\dfrac{2x}{a}={{\left( \dfrac{y}{a} \right)}^{2}}$.
Simplifying the terms, we get $\dfrac{2x}{a}={{\left( \dfrac{y}{a} \right)}^{2}}=\dfrac{{{y}^{2}}}{{{a}^{2}}}$.

Thus, we have ${{y}^{2}}=2ax$.

Hence, we get ${{y}^{2}}=2ax$ as the locus of mid-point of chord of the parabola which passes through the vertex of the parabola.

Note: We can take any point on the parabola of the form $\left( h,k \right)$ and solve the equations to find the mid-point of the chord of the parabola passing through the vertex.