Question

Prove that the locus of the mid-point of a chord of the parabola ${{y}^{2}}=4ax$ which subtends a right angle at the vertex is ${{y}^{2}}=2a(x-4a)$.

Answer 1

Hint: Write the equation of the chord joining two points on the parabola and find the slope of lines joining these two points to the vertex of parabola. Use the fact that the product of slopes of perpendicular lines is $-1$.

Complete step-by-step answer:

Let us consider the parabola ${{y}^{2}}=4ax$. We have to find the locus of mid-point of a chord of the parabola which subtends right angle at the vertex.

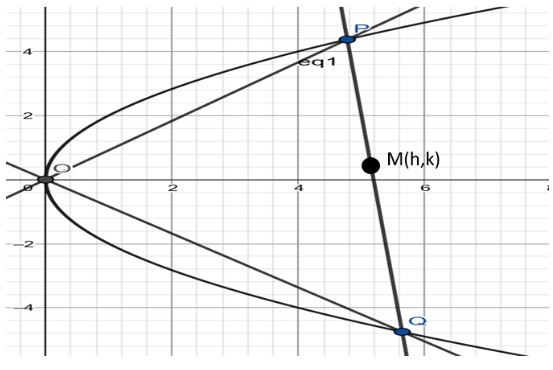
Let’s assume that the chord PQ of the parabola subtends the angle 900 at the vertex $O(0,0)$ of the given parabola.

Let’s assume the co-ordinates of endpoints of the chord are of form $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$.

As the chord $PQ$ subtends ${{90}^{\circ }}$ at the vertex, we have $\angle POQ={{90}^{o}}$.

Thus, we have $OP\bot OQ$.

We will find the slope of lines $OP$ and $OQ$.

We know that the slope of any line with endpoints of the form $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.

Substituting ${{x}_{1}}=0,{{y}_{1}}=0,{{x}_{2}}=at_{1}^{2},{{y}_{2}}=2a{{t}_{1}}$ in the above equation, we get $\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}=\dfrac{2a{{t}_{1}}}{at_{1}^{2}}=\dfrac{2}{{{t}_{1}}}$ as the slope of line $OP$.

Substituting ${{x}_{1}}=0,{{y}_{1}}=0,{{x}_{2}}=at_{2}^{2},{{y}_{2}}=2a{{t}_{2}}$ in the above equation, we get $\dfrac{2a{{t}_{2}}-0}{at_{2}^{2}-0}=\dfrac{2a{{t}_{2}}}{at_{2}^{2}}=\dfrac{2}{{{t}_{2}}}$ as the slope of line $OQ$.

We know that the product of slopes of two perpendicular lines is $-1$.

As we have $OP\bot OQ$, the product of their slopes is$-1$.

Hence, we have $\dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1$.
$\Rightarrow {{t}_{1}}{{t}_{2}}=-4....\left( 1 \right)$

We will now find the mid-point of chord $PQ$.

We know that the mid-point of any two points of the form $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.

Substituting ${{x}_{1}}=at_{1}^{2},{{y}_{1}}=2a{{t}_{1}},{{x}_{2}}=at_{2}^{2},{{y}_{2}}=2a{{t}_{2}}$in the above equation, we get $\left( \dfrac{at_{1}^{2}+at_{2}^{2}}{2},\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2} \right)$as the mid-point of chord $PQ$.

Let’s assume the locus of the mid-point of the chord $PQ$ is $\left( x,y \right)$.
Hence, we have $x=\dfrac{at_{1}^{2}+at_{2}^{2}}{2},y=\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2}=a{{t}_{1}}+a{{t}_{2}}$.

We can rewrite the above equations by rearranging the terms as $\dfrac{2x}{a}=t_{1}^{2}+t_{2}^{2},\dfrac{y}{a}={{t}_{1}}+{{t}_{2}}....\left( 2 \right)$.
We know that we can write $t_{1}^{2}+t_{2}^{2}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}$

Substituting the values of equation $\left( 1 \right)$ and $\left( 2 \right)$ in the above equation, we have $t_{1}^{2}+t_{2}^{2}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-2{{t}_{1}}{{t}_{2}}={{\left( \dfrac{y}{a} \right)}^{2}}-2\left( -4 \right)=\dfrac{{{y}^{2}}}{{{a}^{2}}}+8$.

Substituting the above formula in equation $\left( 2 \right)$, we get $\dfrac{2x}{a}=\dfrac{{{y}^{2}}}{{{a}^{2}}}+8$.

Rearranging the terms by taking LCM, we get ${{y}^{2}}=2ax-8{{a}^{2}}=2a\left( x-4a \right)$.

Hence, the locus of our mid-point of the chord that subtends ${{90}^{\circ }}$ at the vertex of the parabola is ${{y}^{2}}=2a\left( x-4a \right)$.

Note: We can also solve this question by writing the equation of chord in slope form and finding its point of intersection with the parabola to find the locus.