Question

Prove that the locus of the center of a circle, which intercepts a chord of a given length $2a$ on the axis of $x$ and passes through a given point on the axis of $y$ distant $b$ from the origin, is the curve
${{x}^{2}}-2yb+{{b}^{2}}={{a}^{2}}$
Trace this parabola.

Answer 1

Hint: First, find the locus by considering the given condition in the coordinate plane. Then compare it with parabola ${{\left( x-{{x}_{1}} \right)}^{2}}=4a\left( y-{{y}_{1}} \right)$

Complete step-by-step answer:
Let the center of the circle be $\left( h,k \right)$ whose $x$ intercept is equal to $2a$and passes through $\left( a,b \right)$ on the $y$ axis.
Length of chord $AB=2a$.

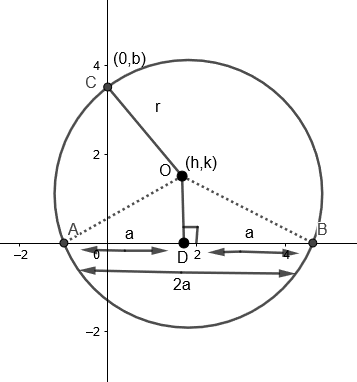
As $\left( h,k \right)$ is center and axis on circumference.
Therefore, $OC=\text{radius = }r$
By distance formula,
$OC=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
$r=\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-b \right)}^{2}}}$
Squaring both sides,
We get ${{r}^{2}}={{h}^{2}}+{{\left( k-b \right)}^{2}}....\left( i \right)$
Construct $OD$ which is perpendicular to $AB$.
As $OA$ and $OB$ are the radius of the circle.
Therefore, $OA=OB=r....\left( ii \right)$
Hence, $\Delta OAB$ is an isosceles triangle.
Therefore, we get $AD=DB=a....\left( iii \right)$
Now by Pythagoras theorem,
$A{{D}^{2}}+D{{O}^{2}}=A{{O}^{2}}$
${{a}^{2}}+{{k}^{2}}={{r}^{2}}\left[ \text{From equation }\left( ii \right)\text{and}\left( iii \right) \right]$
$\Rightarrow {{a}^{2}}+{{k}^{2}}={{h}^{2}}+{{\left( k-b \right)}^{2}}\left[ \text{From equation }\left( i \right) \right]$
Also, $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$
Rearranging the equation we get,
$\Rightarrow {{a}^{2}}+{{k}^{2}}={{h}^{2}}+{{k}^{2}}-2b+{{b}^{2}}$
Or, ${{h}^{2}}-2bk+{{b}^{2}}={{a}^{2}}$
Replacing $h$ with $x$ and $k$ with $y$ to get locus.
$\Rightarrow {{x}^{2}}-2yb+{{b}^{2}}={{a}^{2}}$
Hence proved.
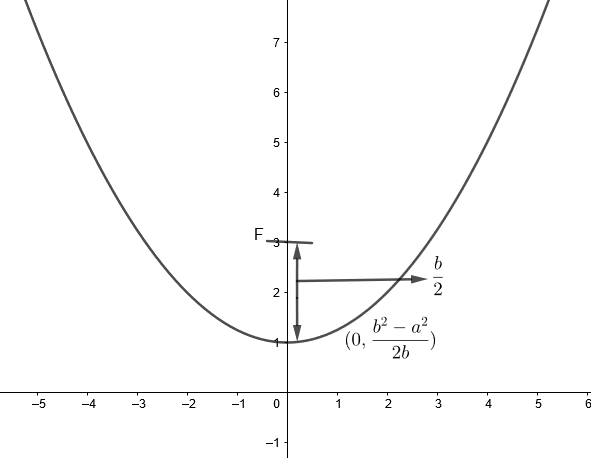
Tracing parabola,
${{x}^{2}}-2yb+{{b}^{2}}={{a}^{2}}$
${{x}^{2}}=2yb+{{a}^{2}}-{{b}^{2}}$
${{x}^{2}}=2b\left[ y-\dfrac{\left( {{b}^{2}}-{{a}^{2}} \right)}{2b} \right]$
Comparing with
${{\left( x-0 \right)}^{2}}=4a{{\left[ y-{{y}_{1}} \right]}^{2}}$
$\therefore$Given parabola has vertex at $\left[ 0,\dfrac{{{b}^{2}}-{{a}^{2}}}{2b} \right]=\left( 0,{{y}_{1}} \right)$and focal length $\left( a \right)=\dfrac{2b}{4}=\dfrac{b}{2}$

Note: Always rearrange the equation to get standard form. Try to get into minimum variables by always taking use of andaxis.