Question

Prove that the locus of intersection of normal at the ends of conjugate diameter is the curve $2{{\left( {{a}^{2}}{{x}^{2}}+{{b}^{2}}{{y}^{2}} \right)}^{3}}={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}{{\left( {{a}^{2}}{{x}^{2}}-{{b}^{2}}{{y}^{2}} \right)}^{2}}$.

Answer 1

Use the concept of conjugate diameters i.e. $\theta -\varphi =\pm \dfrac{\pi }{2}$where $\theta \And \varphi$are eccentric angles of points of conjugate diameter. Write down the equations of normal and eliminate ($\theta \And \varphi$) parametric angles.

Complete answer: Let us first suppose CP and CD are two conjugate diameters.

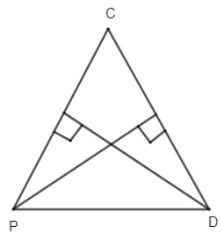
Here we can see that tangent through P is parallel to CD and tangent through D is parallel to PC. Hence, normal to P point is perpendicular to CD and normal to D is perpendicular to PC. Hence, in other words we need to find the orthocentre of $\vartriangle CPD$or intersections of normal.
We have given ellipse; $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-(1)$
Here, we need to assume points of conjugate diameters.
Let $\varphi$is the eccentric angle of point P, then coordinates of $P=\left( a\cos \varphi ,b\sin \varphi \right)$.

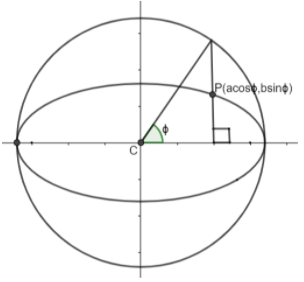
Eccentric angle is the angle between the major axis and line joining the circle at a point where perpendicular from any point to the major axis ellipse is extended to the circle as shown in diagram.
Since CP and CD are conjugate diameters. Hence, tangent at P is parallel to CD as per the definition of conjugate diameter.
Imp point: -
1. We need to know the relation between the two conjugate diameters i.e. If $\left( a\cos \theta ,b\sin \theta \right)$be the coordinates of the extremity of a diameter then $\left( -a\sin \theta ,b\cos \theta \right)$will be the coordinates of the extremity of its conjugate.
It means $\theta -\varphi =\pm \dfrac{\pi }{2}$.
If $\theta$ is an eccentric angle for extremity of a diameter and $\varphi$ is eccentric angle of extremity of other diameter.
Hence, $\vartriangle CPD$ can be represented as

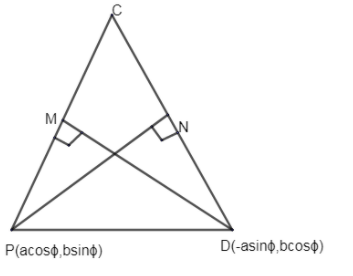
Since, C, P, D are on a circle and $PM\bot CD$, where CD is parallel to the tangent at point P; Hence PM is normal at point P.
Similarly, DN is normal at point D.
Hence, equations of both normal PM & DN respectively are: -
$ax\sec \varphi -by\cos ec\varphi ={{a}^{2}}-{{b}^{2}}-(2)$
(Standard formula for normal through $a\sin \varphi ,b\cos \varphi$)
$-ax\cos ec-by\sec \varphi ={{a}^{2}}-{{b}^{2}}-(3)$
The locus of the orthocentre of $\vartriangle CPD$is obtained by eliminating $\varphi$between (2) and (3)
Apply cross multiplication in following manner: -
$\dfrac{\sec \varphi }{\left( by-ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}=\dfrac{\cos ec\varphi }{\left( by+ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}=\dfrac{-1}{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}$
From the above equation we can write

& \sec \varphi =\dfrac{\left( by-ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}{-\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)} \\\ & \cos ec\varphi =\dfrac{\left( by+ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}{-\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)} \\\ \end{aligned}$$ As we know the relation $${{\sin }^{2}}\varphi +{{\cos }^{2}}\varphi =1$$ $$\begin{aligned} & 1=\dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by-ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}+\dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by+ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}} \\\ & \dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}\left( \dfrac{1}{{{\left( by-ax \right)}^{2}}}+\dfrac{1}{{{\left( by+ax \right)}^{2}}} \right)=1 \\\ & \dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}\times \dfrac{{{\left( by-ax \right)}^{2}}+{{\left( by+ax \right)}^{2}}}{{{\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)}^{2}}}=1 \\\ & 2{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{3}}={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}{{\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)}^{2}} \\\ \end{aligned}$$ Hence proved. **Note:** Terms like auxiliary circle, eccentric angle, orthocentre, conjugate diameters & relation between conjugate diameters should be clearly known otherwise it may take a very long time to solve. Calculation part is also an important one.