Question

Prove that the function $f:N\to X$ defined by $f\left( x \right)={{x}^{2}}$ where $X=\left( y:y={{x}^{2}},x\in N \right)$ is invertible. Also write the inverse of f.

Answer 1

Consider the set of natural numbers (N) as the domain of the function f and the set X as the co-domain of f. To prove that the function is invertible prove that it is both one – one and onto in nature. To prove that the function is one – one, draw the graph of $f\left( x \right)={{x}^{2}}$ and check that not more than one value of x has the same value of $f\left( x \right)$. To check if the function is onto, see if the range and codomain of the function are equal. To write the inverse, write x as a function of y and then equate it with ${{f}^{-1}}\left( y \right)$, replace y with x to get the answer.

Complete step by step answer:
Here we have been provided with the function $f\left( x \right)={{x}^{2}}$ with its domain and co-domain given as $f:N\to X$ and $X=\left( y:y={{x}^{2}},x\in N \right)$. We have to prove that the function is invertible then write its inverse.
Now, a function is invertible if and only if it is both one – one and onto. One – one function means for one value of x there is a single value of $f\left( x \right)$ and onto function means that the range and the co-domain of the function must be equal. Let us check for the nature of the function one by one using the graphical method. The graph of $f\left( x \right)={{x}^{2}}$ is shown below.

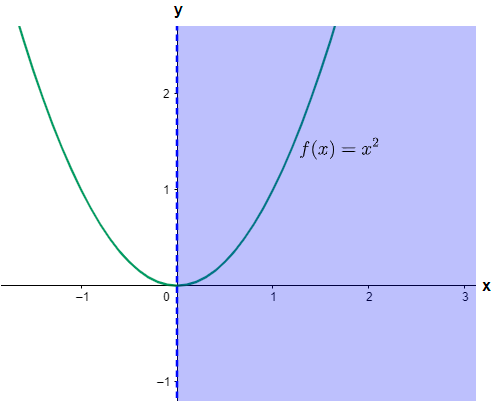
(1) Now, here the domain of the function is the set of all natural numbers (N), from the above graph we can see that if we take only natural numbers as the values of x then for each specific value of x there will be a specific value of $f\left( x \right)$. Therefore the function is one – one in the given domain.
(2) As we can see that the co-domain of the function is X which is given by the relation $X=\left( y:y={{x}^{2}},x\in N \right)$. Clearly we can see that the domain of y in the relation X is also the set of all natural numbers and the function is similar to $f\left( x \right)={{x}^{2}}$, so X will also take the same set of values as taken by $f\left( x \right)$. Therefore the range of $f\left( x \right)$ will be equal to the set of values contained in X. So we have the range = co-domain of the function $f\left( x \right)$. Therefore the function is onto.
We have shown that the function is both one – one and onto and therefore the function $f\left( x \right)$ is invertible. To write its inverse we assume $y=f\left( x \right)$ and therefore we can write $x={{f}^{-1}}\left( y \right)$, so we get,
$\begin{aligned} & \Rightarrow y={{x}^{2}} \\\ & \Rightarrow x=\sqrt{y} \\\ \end{aligned}$
Replacing the value of x with ${{f}^{-1}}\left( y \right)$ we get,
$\Rightarrow {{f}^{-1}}\left( y \right)=\sqrt{y}$
Replacing y with x in the above relation we get,
$\therefore {{f}^{-1}}\left( x \right)=\sqrt{x}$
Hence, the inverse of $f\left( x \right)={{x}^{2}}$ is ${{f}^{-1}}\left( x \right)=\sqrt{x}$.
Note: Note the function $f\left( x \right)={{x}^{2}}$ is not invertible for all real values of x because if we consider all the real values in the domain then there will be values in the domain for which the function will be many – one in nature. For example: if we take x = 1 then $f\left( x \right)=1$, however for x = -1 also we will get $f\left( x \right)=1$ and it will prove that the function is many – one. Also, if we consider all the real values in the co-domain of the function then the function will not be onto because $f\left( x \right)={{x}^{2}}$ cannot give negative values in its range.