Question

Prove that the function defined by $f(x) = \tan x$ is a continuous function.

Answer 1

We prove continuity of the function $\tan x$ by writing in its simpler form of fraction whose continuity is known.

• A continuous function is a function that is continuous on every point of its domain. Also, we can always check continuity by drawing a graph, where the function is continuous means there is no breaking point in the curve.

Complete step-by-step answer:
We know, $\tan x = \dfrac{{\sin x}}{{\cos x}}$
We know graph of $\sin x$ looks like

 ![](https://www.vedantu.com/question-sets/10ff378f-f0a5-4799-8680-c4554bcd598e7775127887609738887.png)  

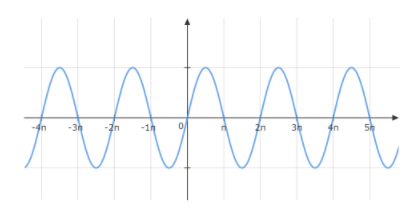
Since, there is no point where the curve breaks, so the function $\sin x$ is continuous everywhere on R
Also, the graph of $\cos x$ looks like.

 ![](https://www.vedantu.com/question-sets/3dca2778-5485-4411-83a9-24b4a087c1c66457509723043121964.png)  

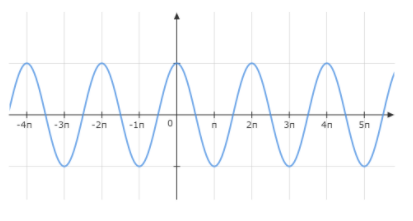
Since, there is no point where the curve breaks, so the function $\cos x$ is continuous everywhere on R.
We know from the algebra of continuous functions that if both $p(x)$ and $q(x)$ are continuous functions then the function defined by their fraction $f(x) = \dfrac{{p(x)}}{{q(x)}}$ is also continuous for all R such that $q(x) \ne 0$
Let us assume $p(x) = \sin x$ and $q(x) = \cos x$
Then by Algebra of continuous functions $f(x) = \dfrac{{\sin x}}{{\cos x}}$ is also continuous everywhere except at points where $q(x) \ne 0$
$\Rightarrow f(x) = \tan x$ is continuous everywhere except at points where $q(x) \ne 0$
Now we find points where $\Rightarrow f(x) = \tan x$ is not continuous.
We have $q(x) \ne 0 \Rightarrow \cos (x) \ne 0$
We will take all other values on R except where the values of $\cos x$ become zero because if we make the denominator zero will make the fraction undefined.

\cos (x) \ne 0 \\\ \cos x \ne \cos (2n + 1)\dfrac{\pi }{2} \\\ x \ne (2n + 1)\dfrac{\pi }{2} \\\ $$ {Since, all odd multiples of $$\dfrac{\pi }{2}$$ will result in $$\cos x = 0$$ } So, $$ \Rightarrow f(x) = \tan x$$ is continuous everywhere except at the points $$x = (2n + 1)\dfrac{\pi }{2}$$, $$n = 0,1,2.....$$ Hence Proved We can draw the graph of the function $$\tan x$$  which is continuous everywhere except all the odd multiples of $$\dfrac{\pi }{2}$$ **Note:** Students many times get confused and write all multiples of $$\dfrac{\pi }{2}$$ have function discontinuous ate them which is wrong, because when we take even multiples of $$\dfrac{\pi }{2}$$, the angles becomes a multiple of $$\pi $$ and which makes $$\cos \pi = - 1$$ but we are finding values of x which make $$\cos x = 0$$, so keep in mind we only take odd multiples of $$\dfrac{\pi }{2}$$ only.