Question

Prove that the equation ${{x}^{2}}+{{y}^{2}}+2(3+p)x+(3-p)y+4=0$ represents a circle for all values of $p$, passing through two fixed points. Find the fixed points.

Answer 1

Hint: For a circle to exist, the centre of the circle should be real, and the radius of the circle should also be real. So the value of ${{g}^{2}}+{{f}^{2}}-c$ should be positive, since the radius is equal to the square root of this very quantity. Imposing these two conditions should get you to the answer.

Complete step by step answer:
First of all, our task is to prove that the equation given above is the equation of a circle. There are two conditions necessary for a circle to exist :
The centre of the circle should be real.
The radius of the circle should be positive and greater than zero. If the radius of the circle is zero, even if the 1st condition is fulfilled, then the equation represents a point, not a circle, or a point circle, more appropriately.
Comparing the equation ${{S}_{1}}={{x}^{2}}+{{y}^{2}}+2(3+p)x+(3-p)y+4=0$ with the general equation of a circle which is : ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$, where the centre of the circle is $(-g,-f)$ and its radius = $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$, we get :
$\begin{aligned} & 2gx=2(3+p)x \\\ & \Rightarrow 2g=2(3+p) \\\ & \Rightarrow g=3+p \\\ \end{aligned}$ and $\begin{aligned} & 2fy=(3-p)y \\\ & \Rightarrow 2f=(3-p) \\\ & \Rightarrow f=\dfrac{3-p}{2} \\\ \end{aligned}$
Thus, the centre ${{C}_{1}}$ of the circle ${{S}_{1}}=(-g,-f)=(-3-p,\dfrac{p-3}{2})$
And its radius ${{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{{{(-3-p)}^{2}}+\dfrac{{{(p-3)}^{2}}}{4}-4}$
Since nowhere in the question is it mentioned that $p$ can take on imaginary values, we’ll assume that it’s always real and this makes the centre of the circle be always real. Thus, the first condition is satisfied.
For the second condition, we need that :
$\begin{aligned} & {{r}_{1}}>0 \\\ & \Rightarrow \sqrt{{{(-3-p)}^{2}}+\dfrac{{{(p-3)}^{2}}}{4}-4}>0 \\\ \end{aligned}$
For this to be true, we need that the quadratic we get after simplifying whatever’s under the root should always be strictly positive. Only when the quadratic is always positive, can it give us a non zero radius, no matter what value of $p$ we use.
Focussing on simplification of the quadratic, we get :
$\begin{aligned} & {{(-3-p)}^{2}}+\dfrac{{{(p-3)}^{2}}}{4}-4>0 \\\ & \Rightarrow 9+{{p}^{2}}+6p+\dfrac{{{p}^{2}}+9-6p}{4}>4 \\\ & \Rightarrow \dfrac{36+4{{p}^{2}}+24p+{{p}^{2}}+9-6p}{4}>4 \\\ & \Rightarrow 36+4{{p}^{2}}+24p+{{p}^{2}}+9-6p>16 \\\ & \Rightarrow 5{{p}^{2}}+18p+29>0 \\\ \end{aligned}$ ………………………………(1)
Thus we have the quadratic, whose value should always be positive.
For a quadratic to always be positive, two conditions need to be fulfilled:
The coefficient of ${{x}^{2}}$ should be positive.
The discriminant, $D$ should be negative.
If the $D$ is negative, this ensures that the graph of the quadratic never cuts the $x$ axis, and thus, it’ll never have any roots, i.e. the quadratic never has zero as a value either, let alone a negative value.
Here’s a graph of equation (1) to demonstrate that it’s always positiv:

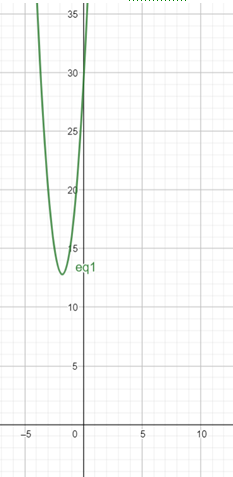
We can thus see that even at the minima, the function’s value doesn’t become $0$ or negative. Hence, the radius of the circle given to us would always be positive.
Thus, for condition 2, we need that the $D$ of equation (1) be negative.
$\begin{aligned} & D={{b}^{2}}-4ac \\\ & D<0 \\\ & \Rightarrow {{b}^{2}}-4ac<0 \\\ & \Rightarrow {{18}^{2}}-4\times 5\times 29<0 \\\ & \Rightarrow 324-580<0 \\\ & \Rightarrow -256<0 \\\ \end{aligned}$
This is always true. Hence, condition 2 is always satisfied for equation (1).
This in turn, satisfies condition 2 of an equation representing a circle, since now, we have successfully proved that the radius is always positive. Thus, the equation given will represent a circle for every value of $p$.
Now moving on to the second part of the question, here we have been asked to find the fixed points that the different circles always pass through, as we keep changing the value of $p$.
We’ll use the concept of family of circles here.
The equation given to us is :${{x}^{2}}+{{y}^{2}}+2(3+p)x+(3-p)y+4=0$
Simplifying the equation we get:
$\begin{aligned} & {{x}^{2}}+{{y}^{2}}+2(3+p)x+(3-p)y+4=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}+2(3)x+(3)y+4+2px-py=0 \\\ & \Rightarrow ({{x}^{2}}+{{y}^{2}}+6x+3y+4)+p(2x-y)=0 \\\ \end{aligned}$ ……………………..(2)
This form shows us that the equation given to us has a form similar to the family of circles that comes from the intersection of a line and a circle.
A family of circles passing through the intersection points of a line and a circle is defined as :${{S}_{1}}+\lambda {{L}_{1}}=0$, where ${{S}_{1}}$ is the equation of the circle and ${{L}_{1}}$ is the equation of the line that cuts the circle, and $\lambda$ is a variable parameter, that decides one particular circle from the family at a time.
To ease your understanding, here’s a graph of the circle ${{S}_{1}}$ and the line ${{L}_{1}}$ cutting it:

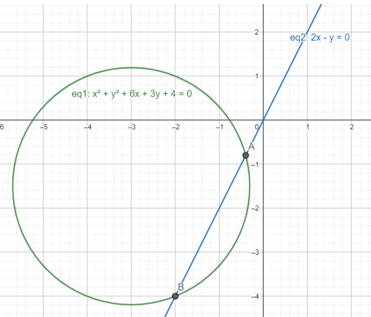
Here, $A$ and $B$ represent the fixed points where the line ${{L}_{1}}$ cuts the circle ${{S}_{1}}$.
Hence, equation (2) can be interpreted as a family of circles, formed by the intersection of a line and a circle, where the circle ${{S}_{1}}:{{x}^{2}}+{{y}^{2}}+6x+3y+4=0$ and the line cutting it, ${{L}_{1}}:2x-y=0$ and $\lambda =p$.
This implies that every circle belonging to this family of circles will pass through the intersection points of the line and the circle definitely, and $\lambda$ will only decide the size and centre of the circle.
Hence, all that’s left for us to do is to find the point of intersection of ${{L}_{1}}$and${{S}_{1}}$.
We can do this by simply substituting for $y$ in ${{S}_{1}}$, using the value of $y$ obtained from ${{L}_{1}}$, in terms of $x$.
$\begin{aligned} & 2x-y=0 \\\ & \Rightarrow y=2x \\\ & S1:{{x}^{2}}+{{y}^{2}}+6x+3y+4=0 \\\ & \Rightarrow {{x}^{2}}+4{{x}^{2}}+6x+6x+4=0 \\\ & \Rightarrow 5{{x}^{2}}+12x+4=0 \\\ & \Rightarrow 5{{x}^{2}}+10x+2x+4=0 \\\ & \Rightarrow 5x(x+2)+2(x+2)=0 \\\ & \Rightarrow (5x+2)(x+2)=0 \\\ & \Rightarrow x=-\dfrac{2}{5},-2 \\\ & \Rightarrow y=2x=-\dfrac{4}{5},-4 \\\ \end{aligned}$
Hence, we have finally obtained the fixed points that every circle belonging to this family passes through, irrespective of the value of $p$.
The points are :$(-\dfrac{2}{5},-\dfrac{4}{5})$ and $(-2,-4)$
Hence proved, the equation represents the equation of a circle and the fixed points all the circles pass through are $(-\dfrac{2}{5},-\dfrac{4}{5})$ and $(-2,-4)$.

Note: The trick to solve the equation given in the problem to represent something similar to the format $S+\lambda L=0$, is to group all terms which have a variable, that is not $x$ or $y$, attached to them, and then the terms which have the common variable, grouped together, will automatically look like the equation of a line. This line cuts the circle which doesn’t have any terms with that common variable attached.