Question

Prove that the equation to the circle passing through the points​ $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$​ and the intersection of the tangents to the parabola at these points is
${{x}^{2}}+{{y}^{2}}-ax\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+2 \right)-ay\left( {{t}_{1}}+{{t}_{2}} \right)\left( 1-{{t}_{1}}{{t}_{2}} \right)+{{a}^{2}}{{t}_{1}}{{t}_{2}}\left( 2-{{t}_{1}}{{t}_{2}} \right)=0$.

Answer 1

There are two points on the parabola where we are trying to find the tangents. So, we use the formula of the equation of tangents for general equations to find the intersecting points. After getting those points with the help of the equation of a circle through endpoints of the chord we create the required equation. Then we put the value of the unknown to get the required equation.

Complete step-by-step solution:
We first try to find the intersecting point of tangents drawn through $P\equiv \left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $Q\equiv \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$​.
The general equation of tangent of parabola ${{y}^{2}}=4ax$ is $y{{t}_{i}}=x+{{x}_{i}}$ where $\left( {{x}_{i}},{{y}_{i}} \right)=\left( a{{t}_{i}}^{2},2a{{t}_{i}} \right)$
Here the value of i runs from 1 to 2. So, $i=1(1)2$.
Then, the equations of the tangents are $y{{t}_{1}}=x+{{x}_{1}}=x+a{{t}_{1}}^{2}$, $y{{t}_{2}}=x+{{x}_{2}}=x+a{{t}_{2}}^{2}$
Solving these two, we have the coordinates of the points of the points of intersection say R as
$y{{t}_{1}}=x+a{{t}_{1}}^{2}\Rightarrow y=\dfrac{x+a{{t}_{1}}^{2}}{{{t}_{1}}}$ and $y{{t}_{2}}=x+a{{t}_{2}}^{2}\Rightarrow y=\dfrac{x+a{{t}_{2}}^{2}}{{{t}_{2}}}$.
So, the intersection is $\dfrac{x+a{{t}_{1}}^{2}}{{{t}_{1}}}=\dfrac{x+a{{t}_{2}}^{2}}{{{t}_{2}}}\Rightarrow x=a{{t}_{1}}{{t}_{2}}$ and $y=\dfrac{a{{t}_{1}}{{t}_{2}}+a{{t}_{1}}^{2}}{{{t}_{1}}}\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right)$.
Let, $R\equiv \left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$.
We know equation of a line passing through two points $\left( m,n \right)$ and $\left( o,p \right)$ will be $\dfrac{y-n}{x-m}=\dfrac{n-p}{m-o}$.
Equation of chord PQ with $P\equiv \left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $Q\equiv \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ will be
$\begin{aligned} & \dfrac{y-2a{{t}_{1}}}{x-a{{t}_{1}}^{2}}=\dfrac{2a{{t}_{1}}-2a{{t}_{2}}}{a{{t}_{1}}^{2}-a{{t}_{2}}^{2}}=\dfrac{2a\left( {{t}_{1}}-{{t}_{2}} \right)}{a\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}} \right)}=\dfrac{2}{\left( {{t}_{1}}+{{t}_{2}} \right)} \\\ & \Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)y-2a{{t}_{1}}\left( {{t}_{1}}+{{t}_{2}} \right)=2x-2a{{t}_{1}}^{2} \\\ & \Rightarrow \left( {{t}_{1}}+{{t}_{2}} \right)y=2x+2a{{t}_{1}}{{t}_{2}} \\\ & \Rightarrow 2x-\left( {{t}_{1}}+{{t}_{2}} \right)y+2a{{t}_{1}}{{t}_{2}}=0 \\\ \end{aligned}$.

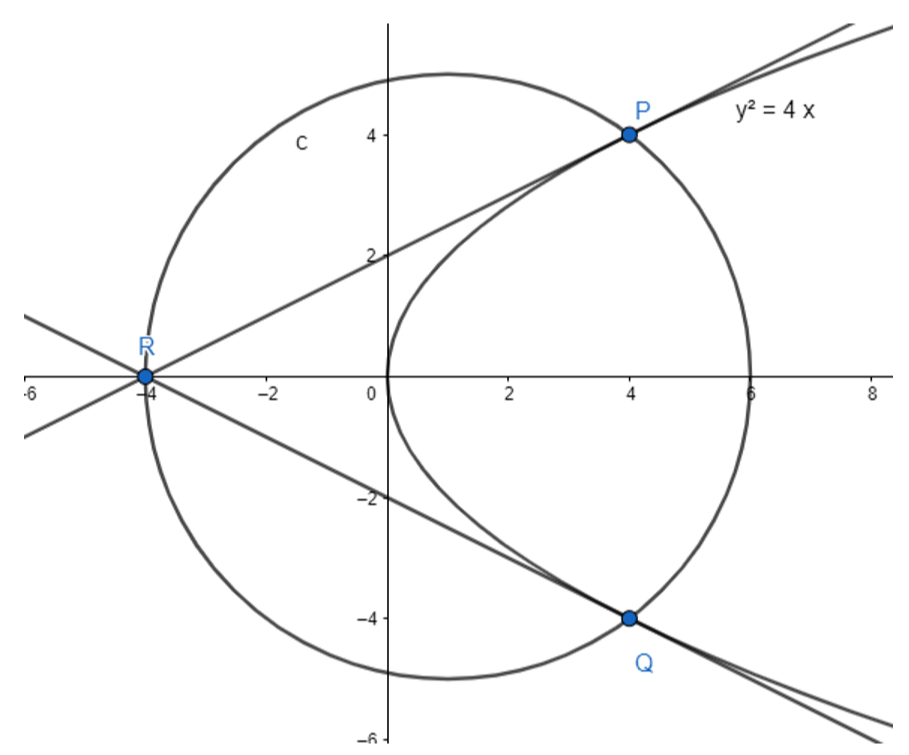
Let the equation of the circle be ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ which is passing through $P\equiv \left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$, $Q\equiv \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ and $R\equiv \left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$.
We put the points in the equation and solve them to find the values of g, f, c.
So, first equation putting $P\equiv \left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ will be
$\begin{aligned} & {{\left( a{{t}_{1}}^{2} \right)}^{2}}+{{\left( 2a{{t}_{1}} \right)}^{2}}+2g\left( a{{t}_{1}}^{2} \right)+2f\left( 2a{{t}_{1}} \right)+c=0 \\\ & \Rightarrow {{a}^{2}}{{t}_{1}}^{4}+4{{a}^{2}}{{t}_{1}}^{2}+2ga{{t}_{1}}^{2}+4fa{{t}_{1}}+c=0........(i) \\\ \end{aligned}$
Second equation putting $Q\equiv \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ will be
$\begin{aligned} & {{\left( a{{t}_{2}}^{2} \right)}^{2}}+{{\left( 2a{{t}_{2}} \right)}^{2}}+2g\left( a{{t}_{2}}^{2} \right)+2f\left( 2a{{t}_{2}} \right)+c=0 \\\ & \Rightarrow {{a}^{2}}{{t}_{2}}^{4}+4{{a}^{2}}{{t}_{2}}^{2}+2ga{{t}_{2}}^{2}+4fa{{t}_{2}}+c=0........(ii) \\\ \end{aligned}$
Third equation putting $R\equiv \left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$ will be
$\begin{aligned} & {{\left( a{{t}_{1}}{{t}_{2}} \right)}^{2}}+{{\left( a\left( {{t}_{1}}+{{t}_{2}} \right) \right)}^{2}}+2g\left( a{{t}_{1}}{{t}_{2}} \right)+2f\left( a\left( {{t}_{1}}+{{t}_{2}} \right) \right)+c=0 \\\ & \Rightarrow {{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}+{{a}^{2}}{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+2ga{{t}_{1}}{{t}_{2}}+2fa\left( {{t}_{1}}+{{t}_{2}} \right)+c=0........(iii) \\\ \end{aligned}$
Now subtracting (ii) from (iii) we get
$\begin{aligned} & {{a}^{2}}{{t}_{2}}^{2}\left( {{t}_{1}}^{2}-{{t}_{2}}^{2} \right)+{{a}^{2}}\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+3{{t}_{2}} \right)+2ga{{t}_{2}}\left( {{t}_{1}}-{{t}_{2}} \right)+2fa\left( {{t}_{1}}-{{t}_{2}} \right)=0 \\\ & \Rightarrow a{{t}_{2}}^{2}\left( {{t}_{1}}+{{t}_{2}} \right)+a\left( {{t}_{1}}+3{{t}_{2}} \right)+2g{{t}_{2}}+2f=0 \\\ & \Rightarrow 2f=-\left( a{{t}_{2}}^{2}\left( {{t}_{1}}+{{t}_{2}} \right)+a\left( {{t}_{1}}+3{{t}_{2}} \right)+2g{{t}_{2}} \right).....(iv) \\\ \end{aligned}$
Now subtracting (i) from (iii) we get
$\begin{aligned} & {{a}^{2}}{{t}_{1}}^{2}\left( {{t}_{2}}^{2}-{{t}_{1}}^{2} \right)+{{a}^{2}}\left( {{t}_{2}}-{{t}_{1}} \right)\left( 3{{t}_{1}}+{{t}_{2}} \right)+2ga{{t}_{1}}\left( {{t}_{2}}-{{t}_{1}} \right)+2fa\left( {{t}_{2}}-{{t}_{1}} \right)=0 \\\ & \Rightarrow a{{t}_{1}}^{2}\left( {{t}_{2}}+{{t}_{1}} \right)+a\left( 3{{t}_{1}}+{{t}_{2}} \right)+2g{{t}_{1}}+2f=0......(v) \\\ \end{aligned}$
We now put the value of 2f in equation (v) from equation (iv).
\begin{aligned} & a{{t}_{1}}^{2}\left( {{t}_{2}}+{{t}_{1}} \right)+a\left( 3{{t}_{1}}+{{t}_{2}} \right)+2g{{t}_{1}}-\left( a{{t}_{2}}^{2}\left( {{t}_{1}}+{{t}_{2}} \right)+a\left( {{t}_{1}}+3{{t}_{2}} \right)+2g{{t}_{2}} \right)=0 \\\ & \Rightarrow a\left( {{t}_{1}}+{{t}_{2}} \right)\left( {{t}_{1}}^{2}-{{t}_{2}}^{2} \right)+2a\left( {{t}_{1}}-{{t}_{2}} \right)+2g\left( {{t}_{1}}-{{t}_{2}} \right)=0 \\\ & \Rightarrow a{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+2a+2g=0 \\\ & \Rightarrow 2g=-\left\\{ 2a+a{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}} \right\\} \\\ \end{aligned}
We got a value of 2g. we put the value in equation (iv)
$\begin{aligned} & 2f=-\left( a{{t}_{2}}^{2}\left( {{t}_{1}}+{{t}_{2}} \right)+a\left( {{t}_{1}}+3{{t}_{2}} \right)+2g{{t}_{2}} \right) \\\ & \Rightarrow 2f=-a{{t}_{2}}^{2}\left( {{t}_{1}}+{{t}_{2}} \right)-a\left( {{t}_{1}}+3{{t}_{2}} \right)+\left( 2a+a{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}} \right){{t}_{2}} \\\ & \Rightarrow 2f=a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right)-a\left( {{t}_{1}}+{{t}_{2}} \right)=a\left( {{t}_{1}}+{{t}_{2}} \right)\left( {{t}_{1}}{{t}_{2}}-1 \right) \\\ \end{aligned}$
We got values of 2g and 2f and we put these values in equation (i) to get

& {{a}^{2}}{{t}_{1}}^{4}+4{{a}^{2}}{{t}_{1}}^{2}+2ga{{t}_{1}}^{2}+4fa{{t}_{1}}+c=0 \\\ & \Rightarrow {{a}^{2}}{{t}_{1}}^{4}+4{{a}^{2}}{{t}_{1}}^{2}+\left\\{ 2a-a{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}} \right\\}a{{t}_{1}}^{2}+2\left\\{ a\left( {{t}_{1}}+{{t}_{2}} \right)\left( {{t}_{1}}{{t}_{2}}-1 \right) \right\\}a{{t}_{1}}+c=0 \\\ & \Rightarrow c={{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}+4{{a}^{2}}{{t}_{1}}{{t}_{2}}-2{{a}^{2}}{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}{{t}_{2}}+1 \right) \\\ \end{aligned}$$ Now, we substitute the value of 2g, 2f, c in the equation of circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. $${{x}^{2}}+{{y}^{2}}-x\left( a{{t}_{1}}^{2}+a{{t}_{2}}^{2}+2a\left( {{t}_{1}}{{t}_{2}}+1 \right) \right)-y\left( 2a{{t}_{1}}+2a{{t}_{2}}-a\left( {{t}_{1}}+{{t}_{2}} \right)\left( {{t}_{1}}{{t}_{2}}+1 \right) \right)+{{a}^{2}}{{t}_{1}}^{2}{{t}_{2}}^{2}+4{{a}^{2}}{{t}_{1}}{{t}_{2}}-2{{a}^{2}}{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}{{t}_{2}}+1 \right)=0$$ Now we simplify the equation to get $$\begin{aligned} & {{x}^{2}}+{{y}^{2}}-x\left( a{{t}_{1}}^{2}+a{{t}_{2}}^{2}+2a{{t}_{1}}{{t}_{2}}+2a \right)-ay\left( {{t}_{1}}-{{t}_{2}}{{t}_{1}}^{2}+{{t}_{2}}-{{t}_{1}}{{t}_{2}}^{2} \right)+{{a}^{2}}\left( -{{t}_{1}}^{2}{{t}_{2}}^{2}+4{{t}_{1}}{{t}_{2}}-2{{t}_{1}}{{t}_{2}} \right)=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-ax\left( \left( {{t}_{1}}^{2}+{{t}_{2}}^{2}+2{{t}_{1}}{{t}_{2}} \right)+2 \right)-ay\left( {{t}_{1}}-{{t}_{2}}{{t}_{1}}^{2}+{{t}_{2}}-{{t}_{1}}{{t}_{2}}^{2} \right)+{{a}^{2}}\left( -{{t}_{1}}^{2}{{t}_{2}}^{2}+4{{t}_{1}}{{t}_{2}}-2{{t}_{1}}{{t}_{2}} \right)=0 \\\ & \Rightarrow {{x}^{2}}+{{y}^{2}}-ax\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+2 \right)-ay\left( {{t}_{1}}+{{t}_{2}} \right)\left( 1-{{t}_{1}}{{t}_{2}} \right)+{{a}^{2}}{{t}_{1}}{{t}_{2}}\left( 2-{{t}_{1}}{{t}_{2}} \right)=0 \\\ \end{aligned}$$ Thus proved $${{x}^{2}}+{{y}^{2}}-ax\left( {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}+2 \right)-ay\left( {{t}_{1}}+{{t}_{2}} \right)\left( 1-{{t}_{1}}{{t}_{2}} \right)+{{a}^{2}}{{t}_{1}}{{t}_{2}}\left( 2-{{t}_{1}}{{t}_{2}} \right)=0$$. **Note:** We need to remember that instead of taking the general equation ${{\left( y-p \right)}^{2}}=4a\left( x-q \right)$ where $\left( p,q \right)$ is the vertex we took ${{y}^{2}}=4ax$. This makes the problem easier as the vertex is irrelevant in this case. Also, we get the equation of the parabola looking at the given parametric coordinates.