Question

Prove that the Earth or the other planets are fastest when they are near the sun. Find the ratio of $\dfrac{{{v_1}}}{{{v_2}}}$ of the planets revolving around the sun.

Answer 1

The above question is divided into two parts. The first part is to prove why the Earth and the other planets speed up near the sun and slow up far from the sun. To answer this question we need to look into Kepler’s laws of planetary motion. The next question is to find the relation between $\dfrac{{{v_1}}}{{{v_2}}}$ the planets. We need to look into the law of conservation of angular momentum.

Complete answer:
Kepler stated three laws of planetary motion. The first law is about the law of orbits. The second law is about the law of equal areas. The third law is about the law of harmony. We need to look into the second law to answer the first part of the question.
The second law of Kepler’s planetary motion states that the planet sweeps equal area in equal intervals of time. This law indicates that the speed at which any planet moves through space is constantly changing. From this law, we can also tell that a planet moves faster when it is closer to the sun and slowest when it moves away from the sun.

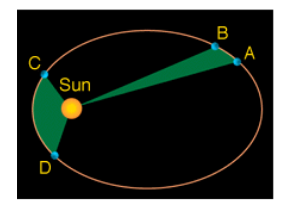
If we analyse the above diagram we can see that the blue planet is moving around the sun. Kepler found that the planet takes same amount time go from point A to point B as it goes from point C to point D. But we can see from the picture that the distance between the point A to B is smaller than the distance between the point C to point D. It has to be in this way so that the green regions have the same area.
That is why the planets must move faster between C and D than that from A to B. Thus from this, we conclude that the planets near the Sun will move faster than the planets far away from the sun.
The second part of the question asks us to find the relation between $\dfrac{{{v_1}}}{{{v_2}}}$ .
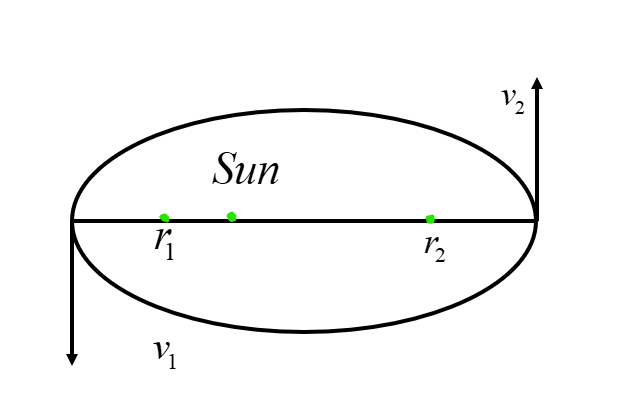
We know that the planet moves around the sun in an elliptical path. This shows us the distance from the sun and the planet in different areas will be different. Hence from the diagram, it is given two radii and two velocities.
${r_1}$ and ${r_2}$ are the distance between the planet and the sun at two different points. ${v_1}$ and ${v_2}$ are the velocities of the planet at the point ${r_1}$ and ${r_2}$ .
We know from the law of conservation of angular momentum,
$\Rightarrow m{v_1}{r_1} = m{v_2}{r_2}$
Cancelling the mass on both sides since they indicate the mass of the same planet we get,
$\Rightarrow {v_1}{r_1} = {v_2}{r_2}$
$\therefore \dfrac{{{v_1}}}{{{v_2}}} = \dfrac{{{r_2}}}{{{r_1}}}$ .

Note:
We can also state Kepler’s second law as “The areal velocity of a planet revolving around the sun in elliptical orbit remains constant. This, in turn, implies that the angular momentum of any planet revolving around the sun remains constant”. Since the angular momentum is constant all planetary motions are called planar motions. This is said to be a direct consequence of central force.