Question

Prove that the area enclosed between two parabolas ${{\text{y}}^2}{\text{ = 4ax}}$ and ${{\text{x}}^2}{\text{ = 4ay}}$ is $\dfrac{{{\text{16}}{{\text{a}}^{\text{2}}}}}{{\text{3}}}$

Answer 1

Here, we find the point of intersection of two given curves by using the given data. Then we find the enclosed area of two parabolas using an integration formula. Finally we get the required answer.

Formula used: The integral formula is
$\int {{{\text{x}}^{\text{n}}}{\text{dx}}} {\text{ = }}\dfrac{{{{\text{x}}^{{\text{n + 1}}}}}}{{{\text{n + 1}}}} + {\text{C}}$, where ${\text{C}}$ is a constant of integration.

Complete step-by-step solution:
It is given that that question stated as the equations of the parabolas are
${{\text{y}}^2}{\text{ = 4ax}}$………………….$(1)$
${{\text{x}}^2}{\text{ = 4ay}}$………………….$(2)$
Here, we have to first find the area of intersection of the two curves:
So that we have to find out the point of intersection of the two curves are
Now from equation $(2)$ we can write it as,
$\Rightarrow \dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{4a}}}}{\text{ = y}}$
On squaring on both sides,
$\Rightarrow {\left( {\dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{4a}}}}} \right)^2}{\text{ = }}{{\text{y}}^2}$
Substitute ${{\text{y}}^2}$ value,
$\Rightarrow {\left( {\dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{4a}}}}} \right)^2}{\text{ = 4ax}}$
$\Rightarrow \left( {\dfrac{{{{\text{x}}^4}}}{{{\text{16}}{{\text{a}}^2}}}} \right){\text{ = 4ax}}$
On taking cross multiplying it,
$\Rightarrow {{\text{x}}^{\text{4}}}{\text{ = 64}}{{\text{a}}^{\text{3}}}{\text{x}}$
On equating this, we get
$\Rightarrow {{\text{x}}^{\text{4}}} - {\text{64}}{{\text{a}}^{\text{3}}}{\text{x}} = 0$
Taking out the common term,
$\Rightarrow {\text{x (}}{{\text{x}}^{\text{3}}}{\text{ - 64}}{{\text{a}}^{\text{3}}}{\text{) = 0}}$
Equate to zero, we get
${\text{x = 0}}$, ${{\text{x}}^{\text{3}}}{\text{ = 64}}{{\text{a}}^{\text{3}}}$
${\text{x = 0}}$, ${\text{x = 4a}}$
Also, we have to find out ${\text{y}}$ values
From equation$(1)$,
$\Rightarrow \dfrac{{{{\text{y}}^{\text{2}}}}}{{{\text{4a}}}}{\text{ = x}}$
Squaring on both sides,
$\Rightarrow {\left( {\dfrac{{{{\text{y}}^{\text{2}}}}}{{{\text{4a}}}}} \right)^2}{\text{ = }}{{\text{x}}^2}$
Substitute ${{\text{x}}^2}$ value,
$\Rightarrow \dfrac{{{{\text{y}}^{\text{4}}}}}{{{\text{16}}{{\text{a}}^{\text{2}}}}}{\text{ = 4ay}}$
Cross multiplying it,
$\Rightarrow {{\text{y}}^{\text{4}}}{\text{ = 64}}{{\text{a}}^{\text{3}}}{\text{y}}$
On equating we get
$\Rightarrow {{\text{y}}^{\text{4}}}{\text{ - 64}}{{\text{a}}^{\text{3}}}{\text{y}} = 0$
Taking out the common term,
$\Rightarrow {\text{y (}}{{\text{y}}^{\text{3}}}{\text{ - 64}}{{\text{a}}^{\text{3}}}{\text{) = 0}}$
${\text{y = 0}}$, ${{\text{y}}^{\text{3}}}{\text{ = 64}}{{\text{a}}^{\text{3}}}$
${\text{y = 0}}$, ${\text{y = 4a}}$
The point of intersection of these two curves are ${\text{(0,0)}}$ and ${\text{(4a,4a)}}$

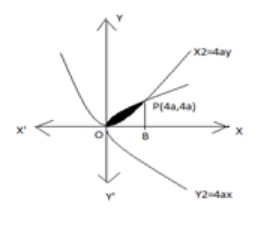
The required areas is A = (area under parabola${{\text{y}}^2}{\text{ = 4ax}}$) – (area under parabola${{\text{x}}^2}{\text{ = 4ay}}$)
From equation (1),
${\text{y = }}\sqrt {{\text{4ax}}}$
From equation (2),
${\text{y = }}\dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{4a}}}}$
Here the limit values are$\left( {0,{\text{ }}4a} \right)$
The enclosed area A = $\int\limits_{\text{0}}^{{\text{4a}}} {{\text{(}}{{\text{y}}_{\text{2}}}{\text{ - }}{{\text{y}}_{\text{1}}}{\text{)dx}}}$
${\text{A = }}\int\limits_{\text{0}}^{{\text{4a}}} {\sqrt {{\text{4ax}}} {\text{dx - }}} \int\limits_{\text{0}}^{{\text{4a}}} {\dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{4a}}}}{\text{dx}}}$
On splitting the term and we get,
$=\int\limits_{\text{0}}^{{\text{4a}}} {{\text{2}}\sqrt {\text{a}} {{\text{x}}^{\dfrac{{\text{1}}}{{\text{2}}}}}{\text{dx}}} {\text{ - }}\int\limits_{\text{0}}^{{\text{4a}}} {\dfrac{{{{\text{x}}^{\text{2}}}}}{{{\text{4a}}}}{\text{dx}}}$
On integrating this we get, (using integration formula)
$={\text{2}}\sqrt{\text{a}}\left({\dfrac{{{\text{2}}{{\text{x}}^{\dfrac{{\text{3}}}{{\text{2}}}}}}}{{\text{3}}}} \right)_{\text{0}}^{{\text{4a}}}{\text{ - }}\left( {\dfrac{{{{\text{x}}^{\text{3}}}}}{{{\text{12a}}}}} \right)_{\text{0}}^{{\text{4a}}}$
Applying upper and lower limit in the ${\text{x}}$ term we get,
$=\dfrac{{{\text{4}}\sqrt{\text{a}}}}{{\text{3}}}{\text{(4}}{{\text{a}}^{\dfrac{{\text{3}}}{{\text{2}}}}}{\text{-0) - }}\left( {\dfrac{{{{{\text{(4a)}}}^{\text{3}}}}}{{{\text{12a}}}}} \right)$
After applying limit, we have,
$\Rightarrow\dfrac{{{\text{4}}\sqrt{\text{a}}}}{{\text{3}}}{\text{(8}}{{\text{a}}^{\dfrac{{\text{3}}}{{\text{2}}}}}{\text{) - }}\dfrac{{{\text{64}}{{\text{a}}^{\text{3}}}}}{{1{\text{2a}}}}$
On simplifying this we get,
$=\dfrac{{{\text{32}}}}{{\text{3}}}{{\text{a}}^{\text{2}}}{\text{-}}\dfrac{{{\text{16}}{{\text{a}}^{\text{2}}}}}{{\text{3}}}$
Take out the common term,
$= \dfrac{{{{\text{a}}^{\text{2}}}}}{{\text{3}}}{\text{(32 - 16)}}$
${\text{A = }}\dfrac{{{\text{16}}{{\text{a}}^{\text{2}}}}}{{\text{3}}}$ Square units

$\therefore$The enclosed area is ${\text{ = }}\dfrac{{{\text{16}}{{\text{a}}^{\text{2}}}}}{{\text{3}}}$ square units

Note: The parabola passes through the origin since $(0,0)$ satisfies the equation ${{\text{y}}^2}{\text{ = 4ax}}$
The parabola is the plane curve which is approximately ‘U’ shaped and mirror-symmetrical.
The curve ${{\text{y}}^2}{\text{ = 4ax}}$ is symmetrical about x-axis and hence ${\text{x}}$-axis or ${\text{y = 0}}$ is the axis of the parabola ${{\text{y}}^2}{\text{ = 4ax}}$
The parabola is symmetric about its axis.
Also, the given axis passing through the focus and the vertex