Question

Prove that $\tan \left( {{\tan }^{-1}}x \right)=x,x\in \mathbb{R}$

Answer 1

Hint : Use the fact that if $y={{\tan }^{-1}}x$ , then $x=\tan y$ . Assume $y={{\tan }^{-1}}x$ . Write $\tan \left( {{\tan }^{-1}}x \right)$ in terms of y and hence prove the above result.

Complete step-by-step answer :
Before dwelling into the proof of the above question, we must understand how ${{\tan }^{-1}}x$ is defined even when $\tan x$ is not one-one.
We know that tanx is a periodic function.
Let us draw the graph of tanx

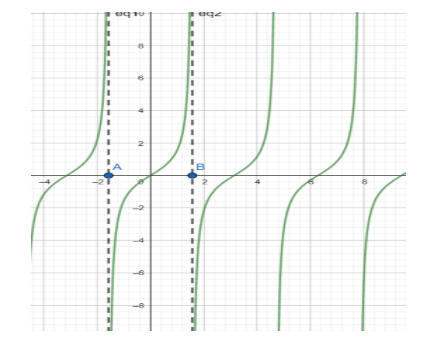
As is evident from the graph tanx is a repeated chunk of the graph of tanx within the interval (A, B) and it attains all its possible values in the interval (A, B)
Hence if we consider tanx in the interval [A, B], we will lose no value attained by tanx, and at the same time, tanx will be one-one and onto.
Hence ${{\tan }^{-1}}x$ is defined over the Domain $\mathbb{R}$ , with codomain $\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$ as in the Domain $\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$ , tanx is one-one and $\text{Range}\left( \tan x \right)=\mathbb{R}$ .
Now since ${{\tan }^{-1}}x$ is the inverse of tanx it satisfies the fact that if $y={{\tan }^{-1}}x$ , then $\tan y=x$ .
So let $y={{\tan }^{-1}}x$
Hence we have tany = x.
Now $\tan \left( {{\tan }^{-1}}x \right)=\tan y$
Hence we have $\tan \left( {{\tan }^{-1}}x \right)=x$ .
Also as x is the Domain of ${{\tan }^{-1}}x$ , we have $x\in \mathbb{R}$ .
Hence $\tan \left( {{\tan }^{-1}}x \right)=x,x\in \mathbb{R}$

Note : [1] The above-specified codomain for arctanx is called principal branch for ${{\tan }^{-1}}x$ . We can select any branch as long as $\tan x$ is one-one and onto and Range $=\mathbb{R}$ . Like instead of $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ , we can select the interval $\left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$ . The proof will remain the same as above.