Solveeit Logo
Login

Question

Question: Prove that $$ \sum_{r=0}^{n} (-1)^r \ ^nC_r \left[ \frac{1}{2^r} + \frac{3^r}{2^{2r}} + \frac{7^r}{2...

Prove that

= \frac{2^{mn}-1}{2^{mn}(2^n-1)}. $$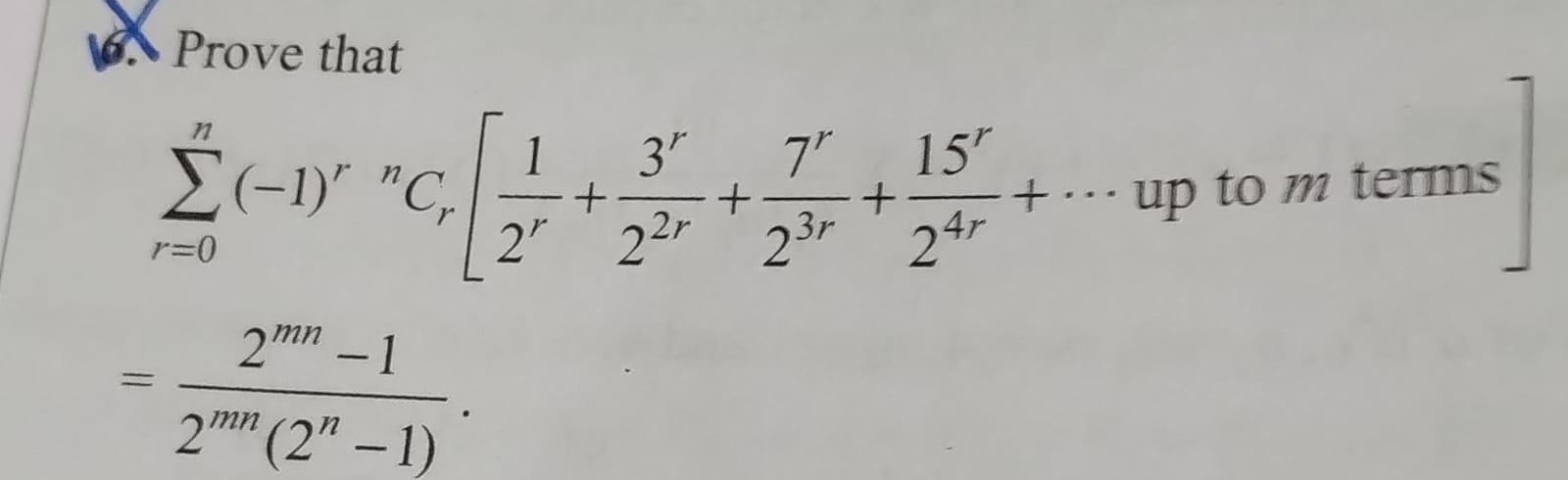
Answer

The identity is proven.

Explanation

Solution

Let the given expression be EE. The terms inside the bracket are (1−12k)r\left(1 - \frac{1}{2^k}\right)^r for k=1,2,…,mk=1, 2, \dots, m. E=∑r=0n(−1)r nCr[∑k=1m(1−12k)r]E = \sum_{r=0}^{n} (-1)^r \ ^nC_r \left[ \sum_{k=1}^{m} \left(1 - \frac{1}{2^k}\right)^r \right] Swapping the order of summation: E=∑k=1m[∑r=0n(−1)r nCr(1−12k)r]E = \sum_{k=1}^{m} \left[ \sum_{r=0}^{n} (-1)^r \ ^nC_r \left(1 - \frac{1}{2^k}\right)^r \right] The inner sum is ∑r=0n nCr(−(1−12k))r=(1−(1−12k))n=(12k)n=12kn\sum_{r=0}^{n} \ ^nC_r (- (1 - \frac{1}{2^k}))^r = \left(1 - (1 - \frac{1}{2^k})\right)^n = \left(\frac{1}{2^k}\right)^n = \frac{1}{2^{kn}}. The outer sum becomes a geometric series: E=∑k=1m12kn=12n⋅1−(12n)m1−12n=12n⋅1−12mn1−12n=2mn−12mn(2n−1)E = \sum_{k=1}^{m} \frac{1}{2^{kn}} = \frac{1}{2^n} \cdot \frac{1 - (\frac{1}{2^n})^m}{1 - \frac{1}{2^n}} = \frac{1}{2^n} \cdot \frac{1 - \frac{1}{2^{mn}}}{1 - \frac{1}{2^n}} = \frac{2^{mn}-1}{2^{mn}(2^n-1)}