Question

Prove that $\sin \theta < \theta < \tan \theta$ for $\theta \in (0,\dfrac{\pi }{2})$.

Answer 1

We will consider a unit circle to prove our given equation. Then we consider a two triangle as per our own interest to find the values of $\sin \theta$ and $\tan \theta$.

Complete step-by-step answer:

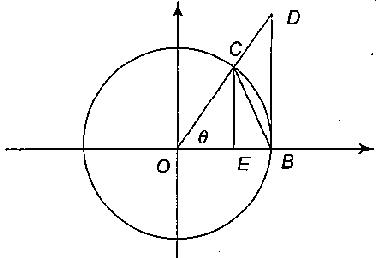
Here we are trying to consider a circle with unit radius with the centre at the origin.
Then we choose a point C on the circumference and another point B on the intersection of the circle and the x axis. Then we draw a perpendicular line from B which is parallel to y axis. We join OC with the perpendicular line in a point D.
Now, the point C is given at random,
From the figure, for any position of C on the circle,
Area of $\Delta OBC$ < Area of sector OBC< Area of $\Delta OBD$
Using the corresponding formulae, the area of the triangle, $\dfrac{1}{2}$.height. base
so, area of \Delta OBC$$$$ = \dfrac{1}{2}.CE.OB, where CE is the height of the triangle of $\Delta OBC$
and area of \Delta OBD$$$$ = \dfrac{1}{2}.DB.OB
and the area of sector OBC, = $\dfrac{1}{2}$. Angle made by the sector OBC. $= \dfrac{1}{2}.\theta$
so, now we have,
$= \dfrac{1}{2}.CE.OB < \dfrac{1}{2}.\theta < \dfrac{1}{2}.DB.OB$
As, for the triangle OCE, $\sin \theta = \dfrac{{CE}}{{OC}} = \dfrac{{CE}}{1} = CE$
And for the triangle ODB, $\tan \theta = \dfrac{{DB}}{{OB}} = \dfrac{{DB}}{1} = DB$
As, $OC = OB = 1$as this is a unit circle,
$= \dfrac{1}{2}.\sin \theta .1 < \dfrac{1}{2}.\theta < \dfrac{1}{2}.\tan \theta .1$
Cancelling out from $\dfrac{1}{2}$ all of them, we get,
$= \sin \theta < \theta < \tan \theta$ for $\theta \in \left( {0,\pi /2} \right)$
Note: In some cases we have also $\sin \theta = \theta$.The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians.