Question

Prove that $\sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x=\sin {{\operatorname{cosec}}^{-1}}\cot {{\tan }^{-1}}x=x$, where $x\in \left[ 0,1 \right]$.

Answer 1

According to the Pythagoras theorem, in a right angled triangle, ${{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Height \right)}^{2}}$. We will use this concept of Pythagoras theorem to change the angle of the trigonometric function. We will first prove $\sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x=x$ and then we will prove $\sin {{\operatorname{cosec}}^{-1}}\cot {{\tan }^{-1}}x=x$ using the trigonometric properties.

Complete step by step answer:
It is given in the question that we have to prove $\sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x=\sin \operatorname{cosec}{{\operatorname{t}}^{-1}}\cot {{\tan }^{-1}}x=x$, where $x\in \left[ 0,1 \right]$. Now, according to the Pythagoras theorem, in a right angled triangle, ${{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Height \right)}^{2}}$. We will use this concept to prove $\sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x=x$ first and then $\sin {{\operatorname{cosec}}^{-1}}\cot {{\tan }^{-1}}x=x$. Let us suppose a triangle with the hypotenuse = 1, base = x, and height = $\sqrt{1-{{x}^{2}}}$. The figure for the same is given below.

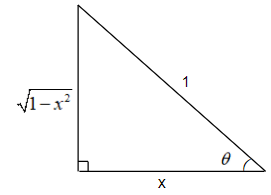
We will change the angle of the trigonometric functions with the help of this triangle. Let us consider the first case, $\sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x$.
From the above triangle, we have the value of $\cos \theta =\dfrac{base}{hypotenuse}=\dfrac{x}{1}=x$ . Also, we can find $\tan \theta =\dfrac{height}{base}=\dfrac{\sqrt{1-{{x}^{2}}}}{x}$ .
Considering the inverse trigonometric function, we can get $\theta ={{\cos }^{-1}}x\text{ and }\theta ={{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}$ .
Now, from the above, it is clear that we can write ${{\cos }^{-1}}x$ as ${{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}$ , so substituting this in place of ${{\cos }^{-1}}x$ in the expression, we get,
$\Rightarrow \sin {{\cot }^{-1}}\tan {{\tan }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}$
We know that $\tan {{\tan }^{-1}}\left( x \right)=x$, so we will apply that and get the above expression as,
$\Rightarrow \sin {{\cot }^{-1}}\dfrac{\sqrt{1-{{x}^{2}}}}{x}$
We know that ${{\cot }^{-1}}x={{\tan }^{-1}}\dfrac{1}{x}$, so applying that, we get,
$\Rightarrow \sin {{\tan }^{-1}}\dfrac{x}{\sqrt{1-{{x}^{2}}}}$
Let us suppose a triangle with the hypotenuse = 1, height = x, and base = $\sqrt{1-{{x}^{2}}}$. The figure for the same is given below.

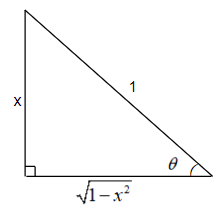
From the above triangle, we can get $\tan \theta =\dfrac{height}{base}=\dfrac{x}{\sqrt{1-{{x}^{2}}}}$ and $\sin \theta =\dfrac{height}{hypotenuse}=\dfrac{x}{1}=x$ . Considering the inverse trigonometric functions, we can write that $\theta ={{\tan }^{-1}}\dfrac{x}{\sqrt{1-{{x}^{2}}}}\text{ and }\theta ={{\sin }^{-1}}x$ .
Now, from the above, it is clear that we can write ${{\tan }^{-1}}\dfrac{x}{\sqrt{1-{{x}^{2}}}}$ as ${{\sin }^{-1}}x$ , so substituting this in place of ${{\sin }^{-1}}x$ in the expression, we get,
$\Rightarrow \sin {{\sin }^{-1}}x$
We know that $\sin {{\sin }^{-1}}x=x$. Thus, finally, we get,
$\Rightarrow \sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x=x$
Now, let us consider the second case, $\sin {{\operatorname{cosec}}^{-1}}\cot {{\tan }^{-1}}x$. We know that ${{\tan }^{-1}}x$ can be written as ${{\cot }^{-1}}\left( \dfrac{1}{x} \right)$. So, we get,
$\Rightarrow \sin {{\operatorname{cosec}}^{-1}}\cot {{\cot }^{-1}}\left( \dfrac{1}{x} \right)$
We know that $\cot {{\cot }^{-1}}x=x$. So, we get,
$\Rightarrow \sin {{\operatorname{cosec}}^{-1}}\left( \dfrac{1}{x} \right)$
We know that $\sin x=\dfrac{1}{{{\operatorname{cosec}}^{-1}}x}$. So, we get,
$\Rightarrow \sin {{\sin }^{-1}}\left( x \right)$
And we know that we can write $\sin {{\sin }^{-1}}\left( x \right)$ as x, so we get,
$\Rightarrow \sin {{\operatorname{cosec}}^{-1}}\cot {{\tan }^{-1}}x=x$
Therefore, we get, $\sin {{\cot }^{-1}}\tan {{\cos }^{-1}}x=\sin {{\operatorname{cosec}}^{-1}}\cot {{\tan }^{-1}}x=x$. Hence, it is proved.

Note: The students may do mistakes while converting the trigonometric functions. We have the term ${{\cos }^{-1}}x$, which can also be written as ${{\cos }^{-1}}\dfrac{x}{1}$. We can suppose it as $\theta$ and take cos on both sides, so we get $\cos \theta =\dfrac{x}{1}$. So, here we can see that x is the base and 1 is the hypotenuse. Therefore, we have considered the sides of the right angled triangle accordingly. This is an important point to consider the sides of the triangle, else we can go wrong.