Question

Prove that ${\sin ^6}\theta + {\cos ^6}\theta + 3{\sin ^2}\theta {\cos ^2}\theta = 1$.

Answer 1

First of all, we will write the formula of cube of sum of two variables which we will require in this formula and then just consider those two quantities to be ${\sin ^2}\theta$ and ${\cos ^2}\theta$ and after simplification, we will get the required answer.

Complete step-by-step answer:
We know that: ${(a + b)^3} = {a^3} + {b^3} + 3ab(a + b)$.
Now, let $a = {\sin ^2}\theta$ and $b = {\cos ^2}\theta$. Putting this in the formula stated above, we will get:-
${({\sin ^2}\theta + {\cos ^2}\theta )^3} = {\left( {{{\sin }^2}\theta } \right)^3} + {\left( {{{\cos }^2}\theta } \right)^3} + 3{\sin ^2}\theta {\cos ^2}\theta ({\sin ^2}\theta + {\cos ^2}\theta )$
We also know that ${\sin ^2}\theta + {\cos ^2}\theta = 1$.
On putting this, we will get:-
$\Rightarrow {(1)^3} = {\left( {{{\sin }^2}\theta } \right)^3} + {\left( {{{\cos }^2}\theta } \right)^3} + 3{\sin ^2}\theta {\cos ^2}\theta (1)$
On simplifying it, we will get:-
$\Rightarrow 1 = {\sin ^6}\theta + {\cos ^6}\theta + 3{\sin ^2}\theta {\cos ^2}\theta$.
We can see that this is the required result.
Hence, proved.

Note: The students must note the fact we used in this which is: ${\sin ^2}\theta + {\cos ^2}\theta = 1$. We can easily prove it as well.
Consider the triangle given below where we have a triangle ABC right angled at A and without loss of generality, we have considered the angle C to be equal to $\theta$.

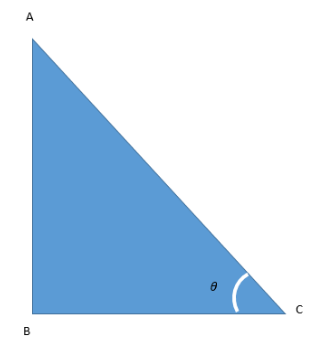
So, here we see that $\sin \theta = \dfrac{P}{H} = \dfrac{{AB}}{{AC}}$ ………(1)
And $\cos \theta = \dfrac{B}{H} = \dfrac{{BC}}{{AC}}$ ………..(2)
Squaring (1), we will get: ${\sin ^2}\theta = {\left( {\dfrac{{AB}}{{AC}}} \right)^2}$ ………(3)
Squaring (2), we will get: ${\cos ^2}\theta = {\left( {\dfrac{{BC}}{{AC}}} \right)^2}$ ………….(4)
Now, adding (3) and (4), we will get:- ${\sin ^2}\theta + {\cos ^2}\theta = {\left( {\dfrac{{AB}}{{AC}}} \right)^2} + {\left( {\dfrac{{BC}}{{AC}}} \right)^2}$.
We can rewrite it as: ${\sin ^2}\theta + {\cos ^2}\theta = \dfrac{{A{B^2}}}{{A{C^2}}} + \dfrac{{B{C^2}}}{{A{C^2}}}$.
Since, the denominator on the RHS is same for both the quantities, we can add the numerator directly.
Hence, we get: ${\sin ^2}\theta + {\cos ^2}\theta = \dfrac{{A{B^2} + B{C^2}}}{{A{C^2}}}$ …………..(5)
Now, we know that the Pythagorean Theorem states that in a right angled triangle, the square of the hypotenuse is equal to the sum of squares of another two sides.
Hence, in this triangle ABC, we will get: $A{B^2} + B{C^2} = A{C^2}$.
Putting this in (5), we will get as follows:-
${\sin ^2}\theta + {\cos ^2}\theta = \dfrac{{A{C^2}}}{{A{C^2}}}$
On simplifying the RHS, we will get: ${\sin ^2}\theta + {\cos ^2}\theta = 1$
Hence, proved.