Question
Question: Prove that: \({{\sin }^{2}}2+{{\cos }^{2}}2=1\)....
Prove that: sin22+cos22=1.
Solution
For solving this question you should know about the general form of trigonometric functions. In this problem we will solve it with the help of a right triangle and applying Pythagoras Theorem on that. That will provide us with the final answer and here we can consider the value of θ as 2.
Complete step by step answer:
According to our question it is asked of us to prove that sin22+cos22=1. Here we can see that this is given in a form of sin2θ+cos2θ=1. So, here we can consider the value of θ as 2. So, now our question is to prove, sin22+cos22=1. For this we will use a right triangle. And then we will apply Pythagoras Theorem for proving this and we will also keep in mind that HP=sinθ and HB=cosθ. Here P stands for perpendicular, H stands for hypotenuse and B stands for base. Now if we make a right triangle as follows,
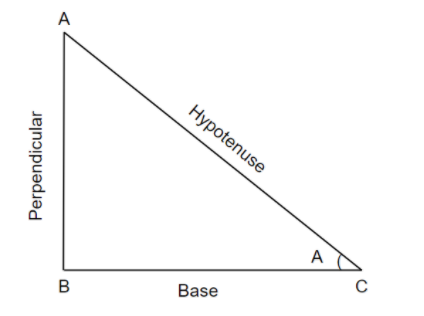
Now, let angle A be θ. We will apply the theorem of Pythagoras Theorem, that is, a2+b2=c2, where a is the value of perpendicular, b is the value of base and c is the value of hypotenuse. So, we will get it as,
perpendicular2+base2=hypotenuse2⇒AB2+BC2=AC2
Dividing the above equation by AC2, we will get,
AC2AB2+BC2=AC2AC2⇒AC2AB2+AC2BC2=1
We know that,
HP=sinθ
HB=cosθ
Now in the equation, AC2AB2+AC2BC2=1,
⇒ACAB=sinθ,ACBC=cosθ
Thus we get the conclusion that,
sin2θ+cos2θ=1
And as we have assumed that θ=2,
So, sin22+cos22=1.
Hence it is proved.
Note: Pythagoras Theorem, that is, perpendicular2+base2=hypotenuse2 is used in this question is the most basic theorem in mathematics and to be used in most questions like this with right angled triangles. Do not forget that, HP=sinθ,HB=cosθ,BP=tanθ.
