Question
Question: Prove that ratio of areas of two similar triangles is equal to the square of ratio of their correspo...
Prove that ratio of areas of two similar triangles is equal to the square of ratio of their corresponding medians.
Solution
Similar triangles: Those triangles whose size can be changed but shape is same is known as similar triangles.
Median: Line segment from vertex to the opposite which bisects that side is median. Every triangle has 3 medians.
Complete step-by-step answer:
Let us take two triangles ABC and PQR where AD is the median in triangle ABC and
PM is the median in the triangle PQR. We have to prove that
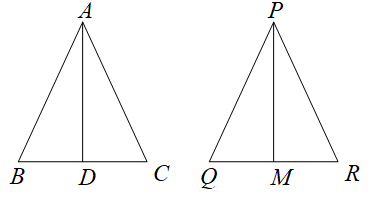
AreaOfΔPQRAreaOfΔABC=(PMAD)2
Proof: Since we are given that two triangles ABC & PQR are similar
∴ ΔABC∼ΔPQR (given)
⇒ ∠B=∠Q (Corresponding angles of similar triangles are also equal)
⇒ PQAB=QRBC (Corresponding scales of similar triangles of same proportion)
\Rightarrow $$$\dfrac{{AB}}{{PQ}} = \dfrac{{BD + DC}}{{QM + MR}} = \dfrac{{BD + BD}}{{QM + QM}}$$ \because AD&PMaremediansSoBD = DC&QM = MR \Rightarrow $$$\dfrac{{AB}}{{PQ}} = \dfrac{{2BD}}{{2QM}} = \dfrac{{BD}}{{QM}}-------(1)
$\therefore $ In $\Delta ABD$ & $\Delta PQM$
$\angle B = \angle Q$ (already proved)
$\dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QM}}$ (From (1)) ----------(2)
$\therefore $ $\Delta ABD \sim \Delta PQM$
$\dfrac{{AB}}{{PQ}} = \dfrac{{DM}}{{PM}}$
Corresponding sides of similar $\Delta $’s in same proportion \dfrac{{AreaOf\Delta ABC}}{{AreaOf\Delta PQR}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2}\dfrac{{AreaOf\Delta ABC}}{{AreaOf\Delta PQR}} = {\left( {\dfrac{{BD}}{{QM}}} \right)^2}$$-----(from equation (2))
Note: 1) From this we can also prove that the ratio of areas of 2 similar Δ’s is equal to the square of ratio of their altitude.
2) Similarity of triangles can be proved by two methods by taking angles and sides.
