Question

Prove that ${{r}_{1}}{{r}_{2}}{{r}_{3}}=r{{s}^{2}}$, where ${{r}_{1}},{{r}_{2}}$and ${{r}_{3}}$is the radius of the exterior circle on side A, B and C.

Answer 1

Hint: Use heron’s formula to solve. Multiply the radius of these circles considered to prove it. Find the radius of ${{r}_{1}},{{r}_{2}}$and ${{r}_{3}}$. Prove the LHS by multiplying ${{r}_{1}},{{r}_{2}}$and ${{r}_{3}}$..

Complete step-by-step answer:
Let us consider that ${{r}_{1}},{{r}_{2}}$and ${{r}_{3}}$are radius of the circle, opposite to a, b and c of the triangle ABC.
Let the triangle be the area of the triangle ABC.
S is the sum of the length of the triangle ABC.
$\therefore s=\dfrac{a+b+c}{2}$
Radius of the triangle, $r=\dfrac{area}{sum-opposite side}$
$\therefore$radius of ${{r}_{1}}=\dfrac{\Delta }{s-a}$
Similarly, ${{r}_{2}}=\dfrac{\Delta }{s-b}$and ${{r}_{3}}=\dfrac{\Delta }{s-c}$
${{r}_{1}}{{r}_{2}}{{r}_{3}}=\left( \dfrac{\Delta }{s-a} \right)\left( \dfrac{\Delta }{s-b} \right)\left( \dfrac{\Delta }{s-c} \right)$
Where radius ${{r}_{1}}$is opposite to the side ‘a’ of $\vartriangle ABC$
radius ${{r}_{2}}$is opposite to the side ‘b’ of $\vartriangle ABC$
radius ${{r}_{3}}$is opposite to the side ‘c’ of $\vartriangle ABC$
$\therefore {{r}_{1}}{{r}_{2}}{{r}_{3}}=\dfrac{{{\Delta }^{3}}}{\left( s-a \right)\left( s-b \right)\left( s-c \right)}-(1)$
By using, Heron’s formula, we can take the area of the triangle, when the length of all three sides of triangle are known:
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}-(2)$
The figure shows the geometrical significance of $\left( s-a \right),\left( s-b \right)$and $\left( s-c \right)$.

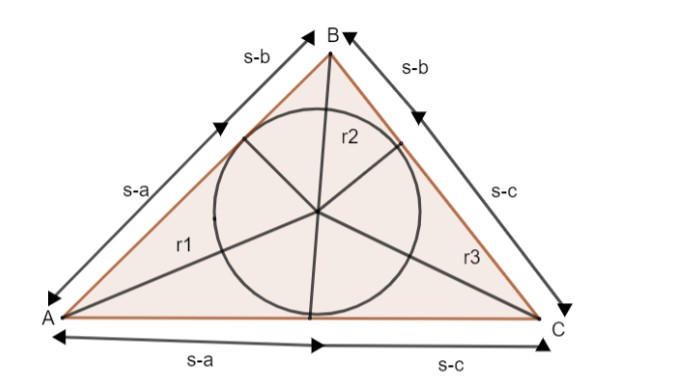
In equation (1) multiply the numerator & denominator by ‘s’.
${{r}_{1}}{{r}_{2}}{{r}_{3}}=\dfrac{{{\Delta }^{3}}\times s}{s\times \left( s-a \right)\left( s-b \right)\left( s-c \right)}-(3)$
We know, $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
Squaring equation (2) on both sides
${{\Delta }^{2}}=s\left( s-a \right)\left( s-b \right)\left( s-c \right)-(4)$
Substitute the value of (4) in (3)
$=\dfrac{s{{\Delta }^{3}}}{{{\Delta }^{2}}}=s\Delta -(5)$
Multiply numerator and denominator by ‘s’ in equation (5)
$={{s}^{2}}\dfrac{\Delta }{s}$
We know the radius in circle, r = a / (sum of lengths of triangle) = $\dfrac{a}{s}$
By substituting the same, we get
${{r}_{1}}{{r}_{2}}{{r}_{3}}=r{{s}^{2}}$.
Note: Remember to use heron’s formula to simplify equation (1).