Question

Prove that \left| {\left( {\begin{array}{*{20}{c}} 0&a;&{ - b}\\\ { - a}&0&{ - c}\\\ b&c;&0 \end{array}} \right)} \right| = 0

Answer 1

Here in this question we have to find a determinant proving that it to be zero.
Formula of determinant: -This is a $3 \times 3$ matrix A = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right) so the determinant is given by
\det A = {a_{11}}\left( {\begin{array}{*{20}{c}} {{a_{22}}}&{{a_{23}}}\\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right) - {a_{12}}\left( {\begin{array}{*{20}{c}} {{a_{21}}}&{{a_{23}}}\\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right) + {a_{13}}\left( {\begin{array}{*{20}{c}} {{a_{21}}}&{{a_{22}}}\\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right)

Complete step-by-step answer:
To solve this equation we will apply a formula of determinant.
\det A = {a_{11}}\left( {\begin{array}{*{20}{c}} {{a_{22}}}&{{a_{23}}}\\\ {{a_{32}}}&{{a_{33}}} \end{array}} \right) - {a_{12}}\left( {\begin{array}{*{20}{c}} {{a_{21}}}&{{a_{23}}}\\\ {{a_{31}}}&{{a_{33}}} \end{array}} \right) + {a_{13}}\left( {\begin{array}{*{20}{c}} {{a_{21}}}&{{a_{22}}}\\\ {{a_{31}}}&{{a_{32}}} \end{array}} \right)
Here matrix is \left| {\left( {\begin{array}{*{20}{c}} 0&a;&{ - b}\\\ { - a}&0&{ - c}\\\ b&c;&0 \end{array}} \right)} \right|
Elements are as follows: -
$\begin{array}{l} {a_{11}} = 0\\\ {a_{12}} = a\\\ {a_{13}} = -b \end{array}$ $\begin{array}{l} {a_{21}} = - a\\\ {a_{22}} = 0\\\ {a_{23}} = - c \end{array}$ $\begin{array}{l} {a_{31}} = b\\\ {a_{32}} = c\\\ {a_{33}} = 0 \end{array}$
Now putting these values in formula we will get
\det A = 0\left( {\begin{array}{*{20}{c}} 0&{ - c}\\\ c&0 \end{array}} \right) - a\left( {\begin{array}{*{20}{c}} { - a}&{ - c}\\\ b&0 \end{array}} \right) + ( - b)\left( {\begin{array}{*{20}{c}} { - a}&0\\\ b&c; \end{array}} \right)
$\det A = 0(0 + {c^2}) - a(0 + bc) + ( - b)( - ac + 0)$
(Cross multiplying from right side lower element to first element of left side then subtracting from left side lower element to first element of right side)
$\det A = 0 - abc + ( - b)( - ac)$
$\det A = - abc + bac$ (Cancelling equal but opposite in sign terms)
$\therefore \det A = 0$
Hence it is proved.

Additional Information: Determinant of a matrix: - Determinant of a matrix is a scalar value which encodes the properties of the linear transformation of the matrix. The determinant of a matrix is denoted by $\det (A)$ Determinant can be viewed as a function whose input is a square matrix but whose output is a number. It is useful for solving linear equations and changing variables in integrals.

Note: Sometimes it is really very confusing to apply this formula so just be patient and only follow some simple rules. Always start from the left side of the matrix and pick the lower element then multiply that element to the top element of the right side then put minus sign and then take lower element of right side and multiply it with top element of left side. It’s just like crisscross. To understand more neatly below is the diagram.

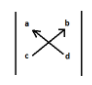
Determinant will be |ad-cb|