Question
Question: Prove that in any triangle, the side opposite to the larger angle is larger....
Prove that in any triangle, the side opposite to the larger angle is larger.
Solution
We know that the sides opposite to the equal sides are equal. Similarly the side opposite to the larger angle is larger.Using this concept we try prove the statement.
Complete step-by-step answer:
Generally this is the theorem that the side opposite to the larger angle is larger. So now let us see how.
Let ABC be a triangle.
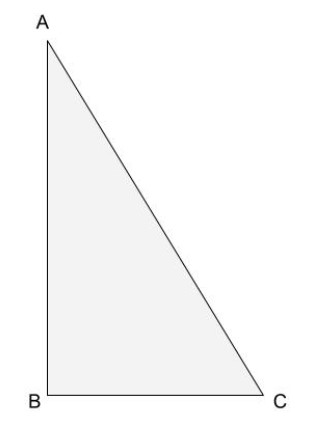
Let us assume that ∠ABC>∠ACB
So if we prove that AC>AB, then it is clear that the side opposite to the larger angle is larger.
For this proof we need the construction.
So construct BD on AC such that ∠DBC=∠ACB
As ∠ABC>∠ACB, so we can find a point on AC that is D such that ∠DBC=∠ACB.
As construction is done, it divides ΔABC into two triangles that are ΔABD and ΔDBC.
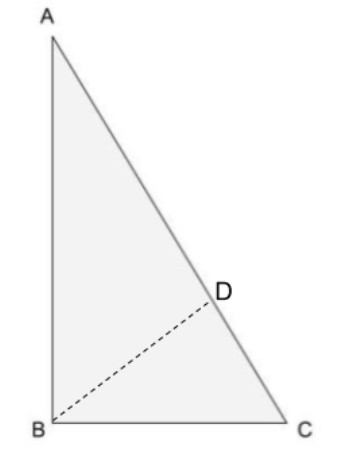
Now in ΔDBC,
∠DBC=∠ACB
As we constructed BD such that the two angles are equal.
Now we know that in the triangle, the sides opposite to equal angles are equal.
So BD=DC −−−−−−−(1)
Now we can add AD on both sides of this above equation,
AD+BD=DC+AD
Now if solve AD+DC, we get AC
So AD+BD=AC
Or we can say that,
AC=BD+AD −−−−−−−(2)
Now in ΔADB,
We know that for any triangle to form, the sum of two sides will always be greater than the third side.
So BD+AD>AB −−−−−−−−(3)
Now putting the value of AD+BD=AC in equation (3),
So we get AC>AB.
Hence it is proved that AC>AB if ∠ABC>∠ACB
Hence we can say that the side opposite to the larger angle is larger.
Note: Let for any triangle ABC, by applying the sin rule we get,
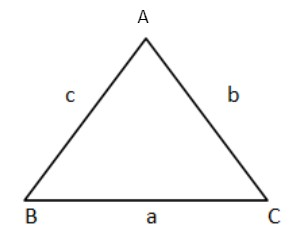
asinA=bsinB=csinC
So if ∠A>∠B,
sinA>sinB as sin is the increasing function.
So asinA=bsinB
a=sinBsinAb and sinA>sinB
So a>b
Hence Proved.
