Question
Question: Prove that for any two sets A and B \(A=\left( A\bigcap B \right)\bigcup \left( A-B \right)\)...
Prove that for any two sets A and B A=(A⋂B)⋃(A−B)
Solution
Hint: Use the fact that A−B=A⋂Bc and apply distributive law of union over the intersection of sets, i.e. A⋃(B⋂C)=(A⋃B)⋂(A⋃C). Use B⋃Bc=U, where U is the universal set and use the fact that if A⊂B then A⋂B=A. Simplify the above expression using these properties of intersection and union of sets.
Complete step-by-step solution -
We know that A−B=A⋂Bc
Hence we have (A⋂B)⋃(A−B)=(A⋂B)⋃(A⋂Bc)
Let C=A⋂B
We have
(A⋂B)⋃(A−B)=C⋃(A⋂Bc)
We know that union distributes over the intersection of two sets. Hence we have
C⋃(A⋂Bc)=(C⋃A)⋂(C⋃Bc)
Now C⋃A=(A⋂B)⋃A
We know that the union of two sets is associative, i.e. A⋃B=B⋃A
Hence we have
C⋃A=A⋃(A⋂B)
Using the distributive law of union over the intersection of two sets, we have
C⋃A=(A⋃A)⋂(A⋃B)
Now we know that A⋃A=A (idempotent law).
Hence we have,
C⋃A=A⋂(A⋃B)
Since A⊂A⋃B,∀B⊂U and A⋂B=A if A⊂B, we have
C⋃A=A
Also, C⋃Bc=(A⋂B)⋃Bc
Using commutative law of union of sets, we have
C⋃Bc=Bc⋃(A⋂B)
Using the distributive law of union over the intersection of sets, we have
C⋃Bc=(Bc⋃A)⋂(Bc⋃B)
We know that Bc⋃B=U
Hence we have
C⋃Bc=(Bc⋃A)⋂U
Since Bc⋃A⊂U, we have
C⋃Bc=Bc⋃A
Hence we have
(A⋂B)⋃(A−B)=(C⋃A)⋂(C⋃Bc)=A⋂(Bc⋃A)
We know that A⊂A⋃B,∀B⊂U
Hence we have
A⊂Bc⋃A
Hence (A⋂B)⋃(A−B)=A
Q.E.D
Note: We can also verify the above result using Venn diagrams
Diagram for A⋂B:
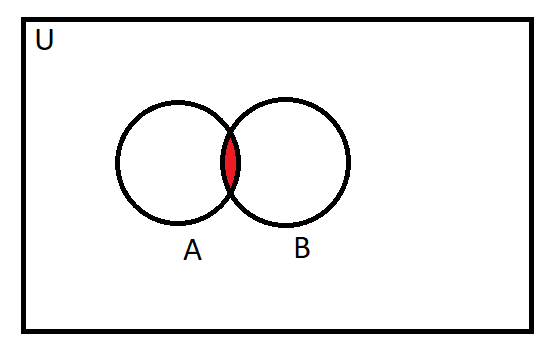
Diagram for A-B:
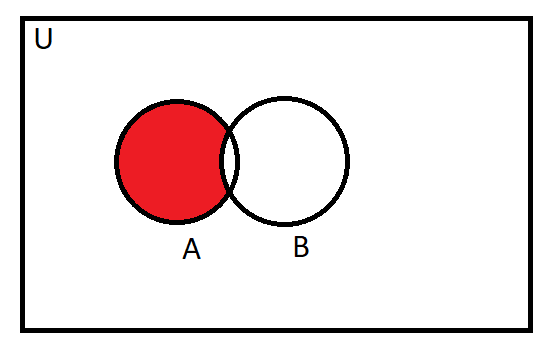
Diagram for (A⋂B)⋃(A−B):
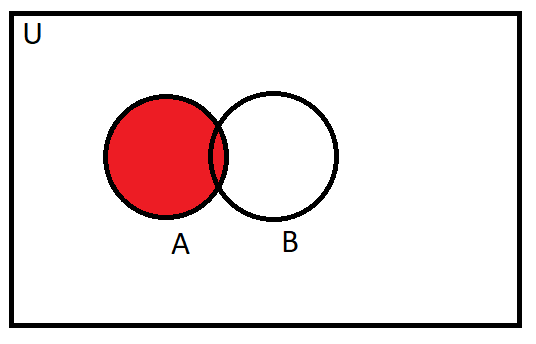
Hence A=(A⋂B)⋃(A−B)
