Question

Prove that $\dfrac{\tan \theta -\cot \theta }{\sin \theta \cos \theta }={{\tan }^{2}}\theta -{{\cot }^{2}}\theta$ .

Answer 1

Hint: Try to simplify the left-hand side of the equation that we need to prove by using the properties that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }\text{ and }\cot \theta =\dfrac{\cos \theta }{\sin \theta }$ , and other related formulas.

Complete step-by-step solution -
Before moving to the solution, let us discuss the periodicity of the secant and tangent function, which we would be using in the solution. All the trigonometric ratios, including secant and tangent, are periodic functions. We can better understand this using the graph of secant and tangent.
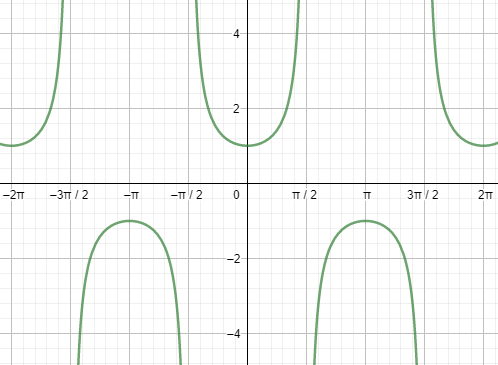
First, let us start with the graph of secx.

Next, let us see the graph of tanx.

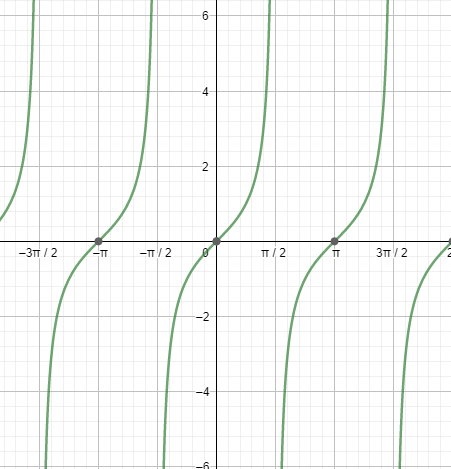
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the secant function and the tangent function is $2{{\pi }^{c}}=360{}^\circ$
We will now solve the left-hand side of the equation given in the question.
$\dfrac{\tan \theta -\cot \theta }{\sin \theta \cos \theta }$
Now we will use the properties that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }\text{ and }\cot \theta =\dfrac{\cos \theta }{\sin \theta }$ . On doing so, we get
$\dfrac{\dfrac{\sin \theta }{\cos \theta }-\dfrac{\cos \theta }{\sin \theta }}{\sin \theta \cos \theta }$
$=\dfrac{{{\sin }^{2}}\theta -{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta {{\cos }^{2}}\theta }$
$=\dfrac{{{\sin }^{2}}\theta }{{{\sin }^{2}}\theta {{\cos }^{2}}\theta }-\dfrac{{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta {{\cos }^{2}}\theta }$
$=\dfrac{1}{{{\cos }^{2}}\theta }-\dfrac{1}{{{\sin }^{2}}\theta }$
Now we know that $\dfrac{1}{\sin \theta }=\cos ec\theta \text{ and }\dfrac{1}{\cos \theta }=\sec \theta$.
$\therefore {{\sec }^{2}}\theta -\cos e{{c}^{2}}\theta$
Also, we know that ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta \text{ and }\cos e{{c}^{2}}\theta =1+{{\cot }^{2}}\theta$ .
$1+{{\tan }^{2}}\theta -1-{{\cot }^{2}}\theta$
$={{\tan }^{2}}\theta -{{\cot }^{2}}\theta$
As we have shown that the left-hand side of the equation given in the question is equal to the right-hand side of the equation in the question. Hence, we can say that we have proved that $\dfrac{\tan \theta -\cot \theta }{\sin \theta \cos \theta }={{\tan }^{2}}\theta -{{\cot }^{2}}\theta$.

Note: Be careful about the calculation and the signs while opening the brackets. The general mistake that a student can make is 1+x-(x-1)=1+x-x-1. Also, you need to remember the properties related to complementary angles and trigonometric ratios.