Solveeit Logo
Login

Question

Question: Prove that \(\dfrac{{\cos ec\left( {{{90}^ \circ } - x} \right)\sin \left( {{{180}^ \circ } - x} \ri...

Prove that cos⁡ec(90∘−x)sin⁡(180∘−x)cot⁡(360∘−x)sec⁡(180∘+x)tan⁡(90∘+x)sin⁡(−x)=1\dfrac{{\cos ec\left( {{{90}^ \circ } - x} \right)\sin \left( {{{180}^ \circ } - x} \right)\cot \left( {{{360}^ \circ } - x} \right)}}{{\sec \left( {{{180}^ \circ } + x} \right)\tan \left( {{{90}^ \circ } + x} \right)\sin \left( { - x} \right)}} = 1

Explanation

Solution

It is known that cos⁡ec(90∘−x)=sec⁡x\cos ec\left( {{{90}^ \circ } - x} \right) = \sec x,sin⁡(180∘−x)=sin⁡x\sin \left( {{{180}^ \circ } - x} \right) = \sin x,cot⁡(360∘−x)=−cot⁡x\cot \left( {{{360}^ \circ } - x} \right) = - \cot x, sec⁡(180∘+x)=−sec⁡x\sec \left( {{{180}^ \circ } + x} \right) = - \sec x,tan⁡(90∘+x)=−cot⁡x\tan \left( {{{90}^ \circ } + x} \right) = - \cot xand sin⁡(−x)=−sin⁡x\sin \left( { - x} \right) = - \sin x. We do this conversion and simplify this if L.H.S will be equal to 1 then it will be proved that L.H.S=R.H.SL.H.S = R.H.S.

Complete step-by-step answer:
L.H.S=cos⁡ec(90∘−x)sin⁡(180∘−x)cot⁡(360∘−x)sec⁡(180∘+x)tan⁡(90∘+x)sin⁡(−x)L.H.S = \dfrac{{\cos ec\left( {{{90}^ \circ } - x} \right)\sin \left( {{{180}^ \circ } - x} \right)\cot \left( {{{360}^ \circ } - x} \right)}}{{\sec \left( {{{180}^ \circ } + x} \right)\tan \left( {{{90}^ \circ } + x} \right)\sin \left( { - x} \right)}}
Substitute cos⁡ec(90∘−x)=sec⁡x\cos ec\left( {{{90}^ \circ } - x} \right) = \sec x,sin⁡(180∘−x)=sin⁡x\sin \left( {{{180}^ \circ } - x} \right) = \sin x,cot⁡(360∘−x)=−cot⁡x\cot \left( {{{360}^ \circ } - x} \right) = - \cot x, sec⁡(180∘+x)=−sec⁡x\sec \left( {{{180}^ \circ } + x} \right) = - \sec x,tan⁡(90∘+x)=−cot⁡x\tan \left( {{{90}^ \circ } + x} \right) = - \cot xand sin⁡(−x)=−sin⁡x\sin \left( { - x} \right) = - \sin x, we get,
⇒sec⁡xsin⁡x(−cot⁡x)(−sec⁡x)(−cot⁡x)(−sin⁡x)\Rightarrow \dfrac{{\sec x\sin x\left( { - \cot x} \right)}}{{\left( { - \sec x} \right)\left( { - \cot x} \right)\left( { - \sin x} \right)}}
As we can see every term get cancelled
∴L.H.S=1\therefore L.H.S = 1
Given R.H.S=1R.H.S = 1
Therefore, L.H.S=R.H.SL.H.S = R.H.Sproved

Note: Some important formula. Try to remember these formulas to solve these types of problems.

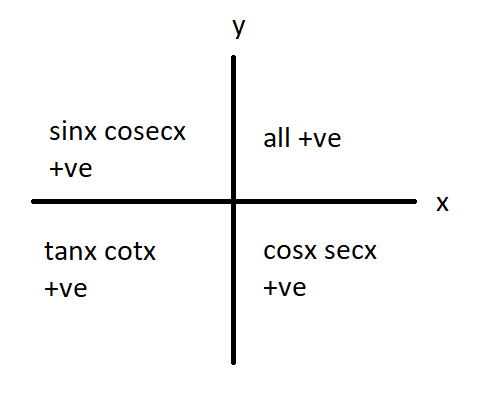
sin⁡(90∘−x)=cos⁡x tan⁡(90∘−x)=cot⁡x cos⁡ec(90∘−x)=sec⁡x cos⁡(90∘−x)=sin⁡x cot⁡(90∘−x)=tan⁡x sec⁡(90∘−x)=cos⁡ecx  \sin ({90^ \circ } - x) = \cos x \\\ \tan ({90^ \circ } - x) = \cot x \\\ \cos ec({90^ \circ } - x) = \sec x \\\ \cos \left( {{{90}^ \circ } - x} \right) = \sin x \\\ \cot \left( {{{90}^ \circ } - x} \right) = \tan x \\\ \sec \left( {{{90}^ \circ } - x} \right) = \cos ecx \\\ sin⁡(90∘+x)=cos⁡x tan⁡(90∘+x)=−cot⁡x cos⁡ec(90∘+x)=sec⁡x cos⁡(90∘+x)=−sin⁡x cot⁡(90∘+x)=−tan⁡x sec⁡(90∘+x)=−cos⁡ecx \sin ({90^ \circ } + x) = \cos x \\\ \tan ({90^ \circ } + x) = - \cot x \\\ \cos ec({90^ \circ } + x) = \sec x \\\ \cos \left( {{{90}^ \circ } + x} \right) = - \sin x \\\ \cot \left( {{{90}^ \circ } + x} \right) = - \tan x \\\ \sec \left( {{{90}^ \circ } + x} \right) = - \cos ecx \\\

sin⁡(180∘+x)=−cos⁡x tan⁡(180∘+x)=cot⁡x cos⁡ec(180∘+x)=−sec⁡x cos⁡(180∘+x)=−sin⁡x cot⁡(180∘+x)=tan⁡x sec⁡(180∘+x)=−cos⁡ecx  \sin ({180^ \circ } + x) = - \cos x \\\ \tan ({180^ \circ } + x) = \cot x \\\ \cos ec({180^ \circ } + x) = - \sec x \\\ \cos \left( {{{180}^ \circ } + x} \right) = - \sin x \\\ \cot \left( {{{180}^ \circ } + x} \right) = \tan x \\\ \sec \left( {{{180}^ \circ } + x} \right) = - \cos ecx \\\

sin⁡(360∘−x)=−cos⁡x tan⁡(360∘−x)=−cot⁡x cos⁡ec(360∘−x)=−sec⁡x cos⁡(360∘−x)=sin⁡x cot⁡(360∘−x)=−tan⁡x sec⁡(360∘−x)=cos⁡ecx  \sin ({360^ \circ } - x) = - \cos x \\\ \tan ({360^ \circ } - x) = - \cot x \\\ \cos ec({360^ \circ } - x) = - \sec x \\\ \cos \left( {{{360}^ \circ } - x} \right) = \sin x \\\ \cot \left( {{{360}^ \circ } - x} \right) = - \tan x \\\ \sec \left( {{{360}^ \circ } - x} \right) = \cos ecx \\\