Question

Prove that $\cos \left( {{\sin }^{-1}}\dfrac{3}{5}+{{\cot }^{-1}}\dfrac{3}{2} \right)=\dfrac{6}{5\sqrt{13}}$ $$$$

Answer 1

We are going to substitute ${{\sin }^{-1}}\dfrac{3}{5}$ with $\alpha$and ${{\cot }^{-1}}\dfrac{3}{2}$ with$\beta$. Then we will use definitions of trigonometric ratios to determine the values required to use in the formula,
$\cos (\alpha +\beta )=\cos \alpha .\cos \beta -\sin \alpha .\sin \beta$.

Complete step by step answer:

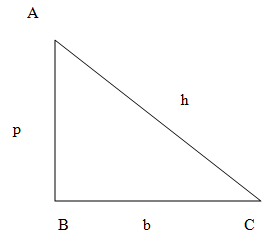
In a right angled-triangle $\Delta \text{ABC}$ we denote the perpendicular $\overline{\text{AB}}$ by $p$, the $\overline{\text{BC}}$ base by $b$ and the hypotenuse $\overline{\text{AC}}$ by $h$.$$$$
From Pythagoras theorem,
${{p}^{2}}+{{b}^{2}}={{h}^{2}}$
Let us also denote$\angle \text{ACB}=\theta$,
Then following the conventional the trigonometric definitions,
$\sin \theta =\dfrac{p}{h},\cos \theta =\dfrac{b}{h},\tan \theta =\dfrac{p}{b},\cot \theta =\dfrac{b}{p}$
Now using Pythagoras theorem,

& {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =\dfrac{{{p}^{2}}}{{{h}^{2}}}+\dfrac{{{b}^{2}}}{{{h}^{2}}}=\dfrac{{{p}^{2}}+{{b}^{2}}}{{{h}^{2}}}=1 \\\ & \Rightarrow \cos \theta =\sqrt{1-{{\sin }^{2}}\theta }=\sqrt{1-\dfrac{{{p}^{2}}}{{{h}^{2}}}}......(1) \\\ \end{aligned}$$ Again, $$\cot \theta =\dfrac{b}{p}=\dfrac{\dfrac{b}{h}}{\dfrac{p}{h}}=\dfrac{\dfrac{b}{\sqrt{{{b}^{2}}+{{p}^{2}}}}}{\dfrac{p}{\sqrt{{{b}^{2}}+{{p}^{2}}}}}=\dfrac{\cos \theta }{\sin \theta }$$ From above we obtain, $$\left. \begin{aligned} & \cos \theta =\dfrac{b}{\sqrt{{{b}^{2}}+{{p}^{2}}}} \\\ & \sin \theta =\dfrac{p}{\sqrt{{{b}^{2}}+{{p}^{2}}}} \\\ \end{aligned} \right\\}........(2)$$ Let us assign ${{\sin }^{-1}}\dfrac{3}{5}=\alpha $ and ${{\cot }^{-1}}\dfrac{3}{2}=\beta $. Now taking $\sin$ both side of ${{\sin }^{-1}}\dfrac{3}{5}=\alpha $ as $$\begin{aligned} & {{\sin }^{-1}}\dfrac{3}{5}=\alpha \\\ & \Rightarrow \sin ({{\sin }^{-1}}\dfrac{3}{5})=\sin \alpha \\\ & \Rightarrow \sin \alpha =\dfrac{3}{5} \\\ & \Rightarrow \text{cos}\alpha =\sqrt{1-{{\sin }^{2}}\alpha }=\sqrt{1-{{\left( \dfrac{3}{5} \right)}^{2}}}=\dfrac{4}{5}\left( \text{from}\left( 1 \right) \right) \\\ \end{aligned}$$ Similarly taking cot both side of ${{\cot }^{-1}}\dfrac{3}{2}=\beta $, $$\begin{aligned} & {{\cot }^{-1}}\dfrac{3}{2}=\beta \\\ & \Rightarrow \cot \left( {{\cot }^{-1}}\dfrac{3}{2} \right)=\cot \beta \\\ & \Rightarrow \cot \beta =\dfrac{3}{2} \\\ & \Rightarrow \cos \beta =\dfrac{3}{\sqrt{{{3}^{2}}+{{2}^{2}}}}=\dfrac{3}{\sqrt{13}},\sin \beta =\dfrac{2}{\sqrt{{{3}^{2}}+{{2}^{2}}}}=\dfrac{2}{\sqrt{13}}\left( \text{from}\left( 2 \right) \right) \\\ & \\\ \end{aligned}$$ Now we have all determined all the values to use in the formula,$\cos (\alpha +\beta )=\cos \alpha .\cos \beta -\sin \alpha .\sin \beta $.$$$$ Now putting all the values in the left hand side of the proof, $$\begin{aligned} & \cos \left( {{\sin }^{-1}}\dfrac{3}{5}+{{\cot }^{-1}}\dfrac{3}{2} \right) \\\ & =\cos \left( \alpha +\beta \right) \\\ & =\cos \alpha \cdot \cos \beta -\sin \alpha \cdot \sin \beta \\\ & =\dfrac{4}{5}\cdot \dfrac{3}{\sqrt{13}}-\dfrac{3}{5}\cdot \dfrac{2}{\sqrt{13}}=\dfrac{6}{5\sqrt{13}} \\\ \end{aligned}$$ The value obtained is equal to the right hand side of the proof. Hence Proved. **Note:** In this problem we need to take care of proper placement during the calculation values while using the formula. The misplacement of values will result in hindrance in proof. We also need to be careful when we are taking inverse of any mathematical function because it may also be possible that the inverse may not be defined. In this problem the value of ${{\sin }^{-1}}\dfrac{3}{5}$ and ${{\cot }^{-1}}\dfrac{3}{2}$ lies domains of $\sin $and $\cot $functions respectively. In other problems if you ever find values which do not lie in the domain know that then the functions are not invertible and you cannot proceed further.