Question

Prove that, any rectangle is a cyclic quadrilateral.

Answer 1

Hint:To prove that any rectangle is a cyclic quadrilateral, we need to prove that the sum of the opposite angles of the quadrilateral is 180 degrees. So, take the sum of opposite angles of the rectangle and show that it is equal to 180 degrees.

Complete step-by-step answer:
Let us see, what a cyclic quadrilateral means?
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively.
Now, one of the most important properties of a cyclic quadrilateral is the supplementary angle property. It says, a quadrilateral is cyclic if and only if its opposite angles are supplementary or 180 degrees.
Now, let us come to the question. We have to prove that, any rectangle is a cyclic quadrilateral.
Assume any rectangle ABCD, we know that all the angles of a rectangle are 90 degrees. Therefore,
$\angle A=\angle B=\angle C=\angle D={{90}^{\circ }}$.

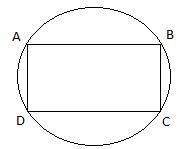
Now, in rectangle ABCD as you can see that angle A and angle C are opposite to each other and angle B and angle D are opposite to each other. Therefore,
$\begin{aligned} & \angle A+\angle C={{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }} \\\ & \text{and, }\angle B+\angle D={{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }} \\\ \end{aligned}$
Clearly, we can see that the sum of opposite angles of the quadrilateral is 180 degrees. Therefore, any rectangle is a cyclic quadrilateral.

Note: One may note that, it is not necessary that a cyclic quadrilateral has sum of its adjacent angles also equal to 180 degrees. In some cases it may be possible, like in the above case of rectangle, but it is not true all the time. So, basically we have to prove that, the sum of opposite angles is 180 degrees.