Question

Prove that an equilateral triangle can be constructed on any given line segment.

Answer 1

We will take a compass, scale and a pencil to do the same. We will first take two points and then draw an arch using the same length as between those points and then join the intersection of those arcs to the two points and thus, we have an equilateral triangle.

Complete step-by-step answer:
Let us say we are given a line as shown below.

Step 1 : Now, mark any two random points A and B on this line. We will get the figure as shown below:

Step 2 : Now, we need to take a compass and put a pencil in it. After that keep the pointed end of the compass at the point A and open it up to the point B.
Now, the pointed sharp end of the compass lies on A and the tip of the pencil is on the point B.

Step 3 : Now, keep the compass opened this much only and keep the pointed end at A and B individually to draw the arch above the line like in the figure given below:

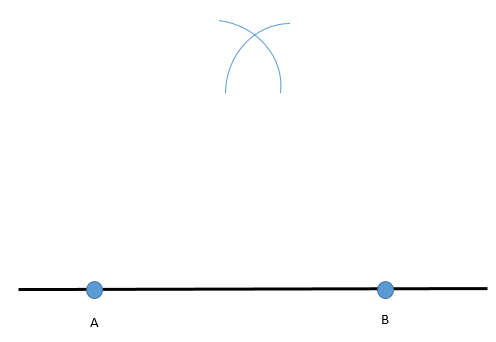
Step 4 : Now, just join the point of intersection of the arcs to both the points A and B like in the figure given below:

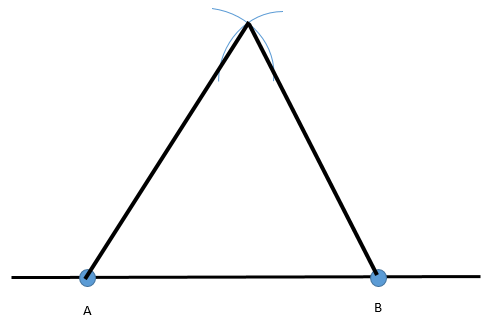
Step 5 : Now, just name the point on the top as C.
We will then eventually get:-
Final Image:-

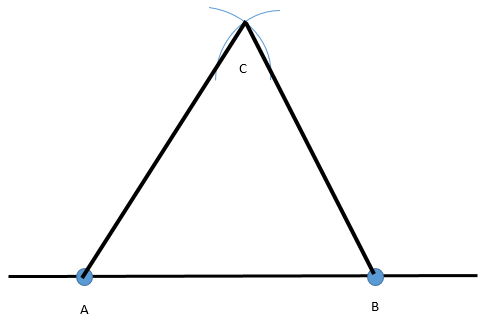
Now, we have ABC as the required equilateral triangle.

Note: The students must note that we did not exactly mention the use of scale / ruler in between but when we joined the point C to the points A and B, we can do that using the ruler / scale only. And, we will also require scale to measure the side of the equilateral triangle.
The students can also verify using the ruler by measuring all the sides and they must be equal to the same number. You can also verify the same using protractor and measuring all the angles to be equal to ${60^ \circ }$.