Question

Prove that
(a) $a(\cos B + \cos C) = 2(b + c){\sin ^2}\dfrac{A}{2}$
(b) $a(\cos C - \cos B) = 2(b - c){\cos ^2}\dfrac{A}{2}$

Answer 1

Here we draw a diagram of a triangle. Use the law of sines to write the ratio of side and sine of the opposite angle. Equate all the ratios to a constant and write the value of sides in terms of constant and sine of the angle.

• Law of sines states that the ratio of length of a side of a triangle to the sine of the opposite angle is the same for all sides and angles.
  (a) Put in values in RHS and change the angle outside the bracket by using the property of sum of angles of a triangle. Use the concept of complementary angles to change the function from sine to cosine. Pair up the values to form combinations for $2\cos x\cos y = \cos (x + y) + \cos (x - y)$ and $2\sin x\cos x = \sin 2x$. Use the quadrant diagram to find the change in function if angle is added or subtracted.
  (b) Put the values in LHS and use the trigonometric identities $\cos x - \cos y = 2\sin \left( {\dfrac{{x + y}}{2}} \right)\sin \left( {\dfrac{{x - y}}{2}} \right)$ and $2\sin x\cos x = \sin 2x$ to open the values. Convert the angles as per requirement by the property of the sum of angles of the triangle. Use the property of complementary angles to change the function from sine to cosine. Pair up the values to use the identity $2\cos x\sin y = \sin (x + y) - \sin (x - y)$ and substitute the values of sine of angles obtained from the equation of law of sines.

Complete step-by-step solution:
We have to draw a triangle with vertices A, B and C. sides opposite to vertices A, B and C are a, b and c respectively.

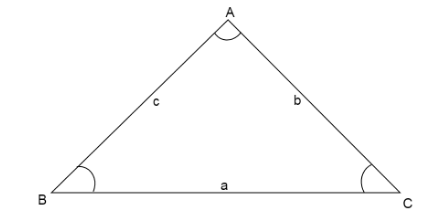
Now we know from sine rule the ratio of length of side to the opposite angle is equal.
Here angle A is opposite to side a, angle B is opposite to b and angle C is opposite to c.
So we can write $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$
Let us assume the ratio is equal to a constant k.
$\Rightarrow \dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k$
Then equating each fraction to k one by one we get
$a = k\sin A$,$b = k\sin B$and$c = k\sin C$.......................… (1)
(a) $a(\cos B + \cos C) = 2(b + c){\sin ^2}\dfrac{A}{2}$
We take Right hand side of the equation.
RHS is$2(b + c){\sin ^2}\dfrac{A}{2}$
Substitute the value of b and c from equation (1)
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2(k\sin B + k\sin C){\sin ^2}\dfrac{A}{2}$
Bring out the common term k outside from the bracket
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2k(\sin B + \sin C){\sin ^2}\dfrac{A}{2}$ ……………...… (2)
Now we know the sum of all angles of a triangle is equal to ${180^ \circ }$
Then $A + B + C = {180^ \circ }$
Shift the sum of angles B and C to RHS of the equation.
$\Rightarrow A = {180^ \circ } - (B + C)$
Substitute the value of angle A in equation (2)
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2k(\sin B + \sin C){\sin ^2}\left( {\dfrac{{{{180}^ \circ } - (B + C)}}{2}} \right)$
Solve the angle in bracket
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2k(\sin B + \sin C){\sin ^2}\left( {\dfrac{{{{180}^ \circ }}}{2} - \dfrac{{(B + C)}}{2}} \right)$
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2k(\sin B + \sin C){\sin ^2}\left( {{{90}^ \circ } - \dfrac{{(B + C)}}{2}} \right)$
Now we know sine and cosine are complementary angles, i.e. $\sin \left( {{{90}^ \circ } - \theta } \right) = \cos \theta$
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2k(\sin B + \sin C){\cos ^2}\left( {\dfrac{{(B + C)}}{2}} \right)$
Use identity $\sin x + \sin y = 2\sin \left( {\dfrac{{x + y}}{2}} \right)\cos \left( {\dfrac{{x - y}}{2}} \right)$to open the term $(\sin B + \sin C)$
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2k\left[ {2\sin \left( {\dfrac{{B + C}}{2}} \right)\cos \left( {\dfrac{{B - C}}{2}} \right)} \right]{\cos ^2}\left( {\dfrac{{(B + C)}}{2}} \right)$
Open the terms in RHS
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = 2 \times k \times 2 \times \sin \left( {\dfrac{{B + C}}{2}} \right) \times \cos \left( {\dfrac{{B - C}}{2}} \right) \times \cos \left( {\dfrac{{B + C}}{2}} \right) \times \cos \left( {\dfrac{{B + C}}{2}} \right)$
We can write
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {2\cos \left( {\dfrac{{B - C}}{2}} \right)\cos \left( {\dfrac{{B + C}}{2}} \right)} \right\\} \times \left\\{ {2\sin \left( {\dfrac{{B + C}}{2}} \right)\cos \left( {\dfrac{{B + C}}{2}} \right)} \right\\}
Apply the trigonometric identity $2\cos x\cos y = \cos (x + y) + \cos (x - y)$to the first bracket and$2\sin x\cos x = \sin 2x$ to the second bracket.
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos \left( {\dfrac{{B - C}}{2} + \dfrac{{B + C}}{2}} \right) + \cos \left( {\dfrac{{B - C}}{2} - \dfrac{{B + C}}{2}} \right)} \right\\} \times \left\\{ {\sin 2\dfrac{{B + C}}{2}} \right\\}
Solve the value of angles inside the bracket
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos \left( {\dfrac{{B - C + B + C}}{2}} \right) + \cos \left( {\dfrac{{B - C - B - C}}{2}} \right)} \right\\} \times \left\\{ {\sin (B + C)} \right\\}
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos \left( {\dfrac{{2B}}{2}} \right) + \cos \left( {\dfrac{{ - 2C}}{2}} \right)} \right\\} \times \left\\{ {\sin (B + C)} \right\\}
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos B + \cos ( - C)} \right\\} \times \left\\{ {\sin (B + C)} \right\\}
We know $\cos ( - x) = \cos x$as cosine is an even function.
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos B + \cos C} \right\\} \times \left\\{ {\sin (B + C)} \right\\}
Substitute the value of$B + C = {180^ \circ } - A$, as sum of angles of triangle is ${180^ \circ }$
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos B + \cos C} \right\\} \times \left\\{ {\sin ({{180}^ \circ } - A)} \right\\}
We know from the quadrant diagram

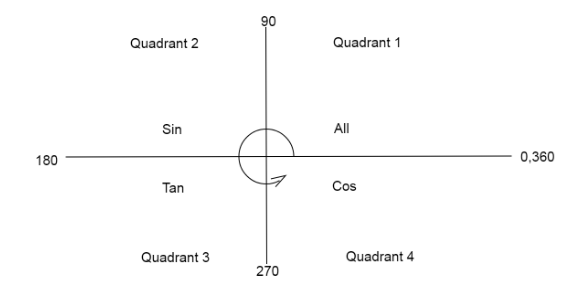
$\sin ({180^ \circ } - \theta ) = \sin \theta$as sine is positive in the second quadrant.
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = k\left\\{ {\cos B + \cos C} \right\\} \times \left\\{ {\sin A} \right\\}
Substitute the value of k from law of sines, $k = \dfrac{a}{{\sin A}}$
\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = \dfrac{a}{{\sin A}} \times \left\\{ {\cos B + \cos C} \right\\} \times \left\\{ {\sin A} \right\\}
Cancel the same terms from numerator and denominator.
$\Rightarrow 2(b + c){\sin ^2}\dfrac{A}{2} = a(\cos B + \cos C)$
So, LHS is equal to RHS
Hence Proved
(b) $a(\cos C - \cos B) = 2(b - c){\cos ^2}\dfrac{A}{2}$
We take Left hand side of the equation.
LHS is$a(\cos C - \cos B)$
Substitute the value of a from equation (1)
$\Rightarrow a(\cos C - \cos B) = k\sin A(\cos C - \cos B)$
Now we know from the trigonometric identity that $\cos x - \cos y = 2\sin \left( {\dfrac{{x + y}}{2}} \right)\sin \left( {\dfrac{{x - y}}{2}} \right)$
Substitute the value of $\cos C - \cos B = 2\sin \left( {\dfrac{{B + C}}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)$
\Rightarrow a(\cos C - \cos B) = k\sin A\left\\{ {2\sin \left( {\dfrac{{B + C}}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
We know$\sin 2x = 2\sin x\cos x$, substitute the value of $\sin A = 2\sin \dfrac{A}{2}\cos \dfrac{A}{2}$
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\sin \dfrac{A}{2}\cos \dfrac{A}{2}} \right\\}\left\\{ {2\sin \left( {\dfrac{{B + C}}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
We know that sum of all angles of triangle is ${180^ \circ }$
Then $A + B + C = {180^ \circ }$
Shift the angle A to RHS of the equation.
$\Rightarrow B + C = {180^ \circ } - A$
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\sin \dfrac{A}{2}\cos \dfrac{A}{2}} \right\\}\left\\{ {2\sin \left( {\dfrac{{{{180}^ \circ } - A}}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
Solve angle in the bracket
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\sin \dfrac{A}{2}\cos \dfrac{A}{2}} \right\\}\left\\{ {2\sin \left( {{{90}^ \circ } - \dfrac{A}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
Since, sine and cosine are complementary angles, i.e. $\sin ({90^ \circ } - \theta ) = \cos \theta$
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\sin \dfrac{A}{2}\cos \dfrac{A}{2}} \right\\}\left\\{ {2\cos \left( {\dfrac{A}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
Similarly, we can write $A = {180^ \circ } - (B + C)$
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\sin \left( {\dfrac{{{{180}^ \circ } - (B + C)}}{2}} \right)\cos \dfrac{A}{2}} \right\\}\left\\{ {2\cos \left( {\dfrac{A}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
Solve the angle in the bracket
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\sin \left( {{{90}^ \circ } - \dfrac{{(B + C)}}{2}} \right)\cos \dfrac{A}{2}} \right\\}\left\\{ {2\cos \left( {\dfrac{A}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
Since, sine and cosine are complementary angles, then
\Rightarrow a(\cos C - \cos B) = k\left\\{ {2\cos \left( {\dfrac{{B + C}}{2}} \right)\cos \dfrac{A}{2}} \right\\}\left\\{ {2\cos \left( {\dfrac{A}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
We can write
\Rightarrow a(\cos C - \cos B) = 2k\left\\{ {2\cos \left( {\dfrac{{B + C}}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}\left\\{ {\cos \left( {\dfrac{A}{2}} \right)\cos \left( {\dfrac{A}{2}} \right)} \right\\}
\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left\\{ {2\cos \left( {\dfrac{{B + C}}{2}} \right)\sin \left( {\dfrac{{B - C}}{2}} \right)} \right\\}
Use the trigonometric identity $2\cos x\sin y = \sin (x + y) - \sin (x - y)$in the bracket
\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left\\{ {\sin \left( {\dfrac{{B + C}}{2} + \dfrac{{B - C}}{2}} \right) - \sin \left( {\dfrac{{B + C}}{2} - \dfrac{{B - C}}{2}} \right)} \right\\}
Solve the angles in the bracket
\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left\\{ {\sin \left( {\dfrac{{B + C + B - C}}{2}} \right) - \sin \left( {\dfrac{{B + C - B + C}}{2}} \right)} \right\\}
\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left\\{ {\sin \left( {\dfrac{{2B}}{2}} \right) - \sin \left( {\dfrac{{2C}}{2}} \right)} \right\\}
\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left\\{ {\sin B - \sin C} \right\\}
We know from law of sines $\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k$
Equating each fraction to k, we can write
$\sin B = \dfrac{b}{k}$and$\sin C = \dfrac{c}{k}$
$\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left( {\dfrac{b}{k} - \dfrac{c}{k}} \right)$
Take LCM in bracket
$\Rightarrow a(\cos C - \cos B) = 2k{\cos ^2}\left( {\dfrac{A}{2}} \right)\left( {\dfrac{{b - c}}{k}} \right)$
Cancel the same terms from numerator and denominator.
$\Rightarrow a(\cos C - \cos B) = 2(b - c){\cos ^2}\left( {\dfrac{A}{2}} \right)$
So, LHS is equal to RHS
Hence Proved

Note: Students many times get confused while checking the value of function from quadrant diagram. Keep in mind we move in anticlockwise direction when adding angles and clockwise direction when subtracting angles. Also, don’t get confused with complementary angles and complementary functions, many students tend to write $\cos \theta = {90^ \circ } - \sin \theta$ which is wrong, the sum of angles is supposed to be ${90^ \circ }$.