Question
Question: Prove that $4 \leq \int_{1}^{3} \sqrt{3+x^2} dx \leq 4\sqrt{3}$...
Prove that 4≤∫133+x2dx≤43
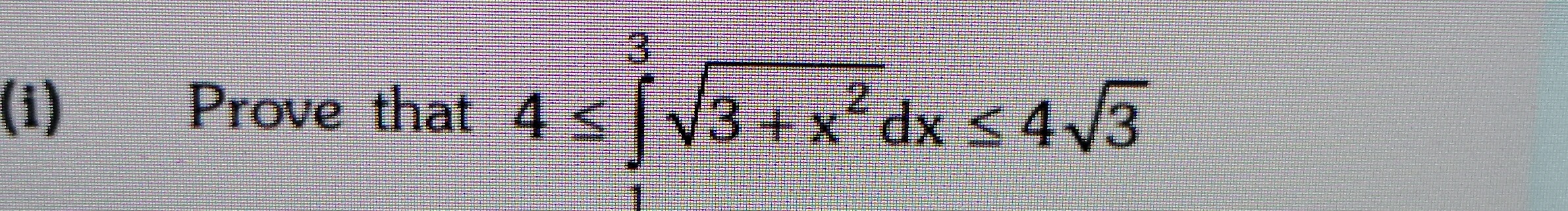
Answer
The statement is true.
Explanation
Solution
Let f(x)=3+x2. The function f(x) is increasing on [1,3] because its derivative f′(x)=3+x2x is positive for x∈[1,3]. The minimum value of f(x) on [1,3] is m=f(1)=3+12=2. The maximum value of f(x) on [1,3] is M=f(3)=3+32=12=23. Using the property m(b−a)≤∫abf(x)dx≤M(b−a), with a=1 and b=3, we get: 2(3−1)≤∫133+x2dx≤23(3−1) 4≤∫133+x2dx≤43
