Question

Prove that: $2sin^2 27 = cos36 - cos54$

Answer 1

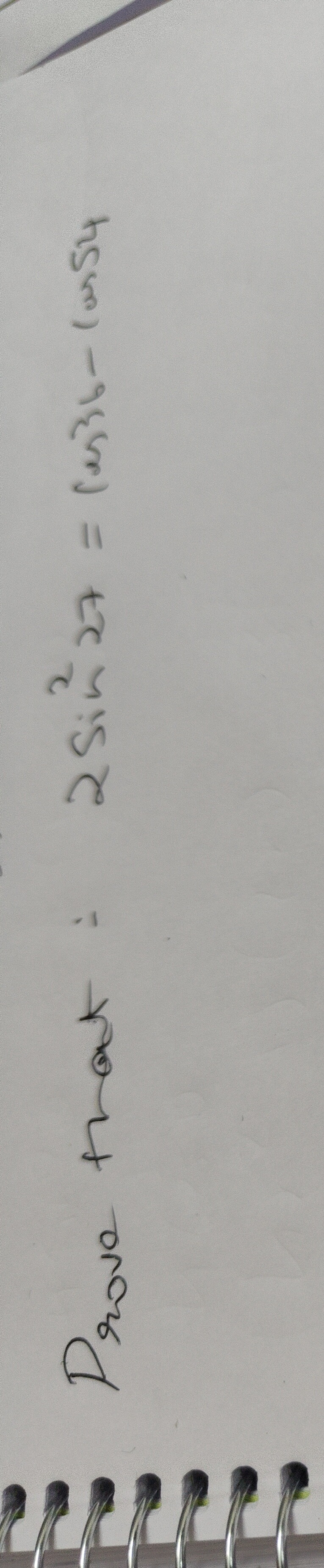
The identity is false.

Answer 2

To prove the given identity $2\sin^2 27^\circ = \cos 36^\circ - \cos 54^\circ$.

Let's evaluate the Left Hand Side (LHS) and the Right Hand Side (RHS) separately.

Left Hand Side (LHS): Using the double angle identity $2\sin^2 \theta = 1 - \cos 2\theta$: LHS $= 2\sin^2 27^\circ = 1 - \cos (2 \times 27^\circ) = 1 - \cos 54^\circ$.

Right Hand Side (RHS): RHS $= \cos 36^\circ - \cos 54^\circ$.

For the given identity to be true, we must have LHS = RHS. So, we need to prove: $1 - \cos 54^\circ = \cos 36^\circ - \cos 54^\circ$

Adding $\cos 54^\circ$ to both sides of the equation: $1 = \cos 36^\circ$

Now, let's check the value of $\cos 36^\circ$. It is a standard trigonometric value: $\cos 36^\circ = \frac{\sqrt{5}+1}{4}$

Since $\frac{\sqrt{5}+1}{4} \neq 1$, the statement $1 = \cos 36^\circ$ is false. Therefore, the original identity $2\sin^2 27^\circ = \cos 36^\circ - \cos 54^\circ$ is false.

Conclusion: The given identity $2\sin^2 27^\circ = \cos 36^\circ - \cos 54^\circ$ is incorrect.