Question

Prove that $2{{\sin }^{2}}\dfrac{\pi }{6}+{{\operatorname{cosec}}^{2}}\dfrac{7\pi }{6}{{\cos }^{2}}\dfrac{\pi }{3}=\dfrac{3}{2}$.

Answer 1

To prove the above trigonometric equation, first of all we have to start solving from the left-hand side. Then convert the equation by replacing $\pi$with ${{180}^{\circ }}$. After that we can solve $\operatorname{cosec}{{210}^{\circ }}$, but before that we can first find the value for $\sin {{210}^{\circ }}$ and then find $\operatorname{cosec}{{210}^{\circ }}$ by taking the reciprocal of $\sin {{210}^{\circ }}$. Then substitute the values and square the values. Then we have to solve it to reach the final answer.

Complete step-by-step answer :
First of all we have to start from the left-hand side, so,
L.H.S: $2{{\sin }^{2}}\dfrac{\pi }{6}+{{\operatorname{cosec}}^{2}}\dfrac{7\pi }{6}{{\cos }^{2}}\dfrac{\pi }{3}$.
Now, we have to put $\pi ={{180}^{\circ }}$, so we get,
$2{{\sin }^{2}}\dfrac{{{180}^{\circ }}}{6}+{{\operatorname{cosec}}^{2}}\dfrac{7\times {{180}^{\circ }}}{6}{{\cos }^{2}}\dfrac{{{180}^{\circ }}}{3}$
On further solving, we get,
$2{{\sin }^{2}}{{30}^{\circ }}+{{\operatorname{cosec}}^{2}}{{210}^{\circ }}{{\cos }^{2}}{{60}^{\circ }}$
Now, we know the value of $\sin {{30}^{\circ }}$ and $\cos {{60}^{\circ }}$, but we have to find the value of $\operatorname{cosec}{{210}^{\circ }}$. To find that value, first we have to find the value of $\sin {{210}^{\circ }}$.
We can write $\sin {{210}^{\circ }}$ as,
$\sin {{210}^{\circ }}=\sin (180+30)$
$\Rightarrow -\sin {{30}^{\circ }}$
$\Rightarrow -\dfrac{1}{2}$
We got $\sin (180+30)=\dfrac{-1}{2}$ because $\sin (180+30)$lies in the third quadrant and in the third quadrant the value of sin is negative. That is why $\sin (180+30)=\dfrac{-1}{2}$. We have to remember the signs of the trigonometric function in each quadrant

As we have got the value of $\sin {{210}^{\circ }}$, we can find the value of $\operatorname{cosec}{{210}^{\circ }}$ by taking the reciprocal of $\sin {{210}^{\circ }}$.

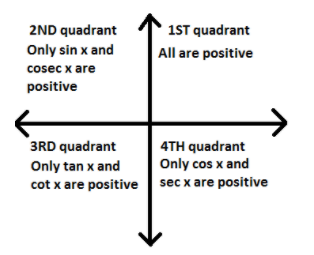
So, the value of $\operatorname{cosec}{{210}^{\circ }}=\left( \dfrac{1}{\left( \dfrac{-1}{2} \right)} \right)=-2$.
Now, we can write as,
L.H.S: $2{{\sin }^{2}}\dfrac{\pi }{6}+{{\operatorname{cosec}}^{2}}\dfrac{7\pi }{6}{{\cos }^{2}}\dfrac{\pi }{3}$
$\Rightarrow 2{{\sin }^{2}}{{30}^{\circ }}+{{\operatorname{cosec}}^{2}}{{210}^{\circ }}{{\cos }^{2}}{{60}^{\circ }}$
We know the value of $\sin {{30}^{\circ }}=\dfrac{1}{2}$ and $\cos {{60}^{\circ }}=\dfrac{1}{2}$. On substituting the values we get,
$\Rightarrow 2{{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( -2 \right)}^{2}}\times {{\left( \dfrac{1}{2} \right)}^{2}}$
On solving, we get,
$\Rightarrow 2\left( \dfrac{1}{4} \right)+4\times \left( \dfrac{1}{4} \right)$
On further solving, we get
$\Rightarrow \left( \dfrac{1}{2} \right)+1$
$\Rightarrow \dfrac{3}{2}=R.H.S$
Hence proved that $2{{\sin }^{2}}\dfrac{\pi }{6}+{{\operatorname{cosec}}^{2}}\dfrac{7\pi }{6}{{\cos }^{2}}\dfrac{\pi }{3}=\dfrac{3}{2}$.

Note : The alternative method for finding $\sin {{210}^{\circ }}$ is that, it can also be written as,
$\sin {{210}^{\circ }}=\sin (270-60)$
We know that, $\sin (270-60)=-\cos {{60}^{\circ }}$
Therefore, we get the value of $\sin {{210}^{\circ }}$ is $-\dfrac{1}{2}$.
So, it is important to keep in mind the changes of sign in each quadrant.