Question

Prove that:
$2{\sin ^2}\dfrac{{3\pi }}{4} + 2{\cos ^2}\dfrac{\pi }{4} + 2{\sec ^2}\dfrac{\pi }{3} = 10$

Answer 1

Note that, ${\text{since }}\dfrac{{3\pi }}{4}{\text{ is in second quadrant, therefore sin}}\dfrac{{3\pi }}{4}{\text{ is positive}}{\text{.}}$
Then in the left hand side, substitute the values of $\sin \dfrac{{3\pi }}{4}$, $\cos \dfrac{\pi }{4}$ and $\sec \dfrac{\pi }{3}$.
In solving it we will reach our desired solution.

Complete step-by-step answer:
Given that, to prove $2{\sin ^2}\dfrac{{3\pi }}{4} + 2{\cos ^2}\dfrac{\pi }{4} + 2{\sec ^2}\dfrac{\pi }{3} = 10$
Left hand side:
$= 2{\sin ^2}\dfrac{{3\pi }}{4} + 2{\cos ^2}\dfrac{\pi }{4} + 2{\sec ^2}\dfrac{\pi }{3}$
The above expression can be written as,
$= 2{\sin ^2}\left( {\pi - \dfrac{\pi }{4}} \right) + 2{\cos ^2}\dfrac{\pi }{4} + 2{\sec ^2}\dfrac{\pi }{3}$
Since $\dfrac{{3\pi }}{4}$ is in the second quadrant, therefore ${\text{sin}}\dfrac{{3\pi }}{4}$ is positive
$= 2{\left( {\sin \dfrac{\pi }{4}} \right)^2} + 2{\cos ^2}\dfrac{\pi }{4} + 2{\sec ^2}\dfrac{\pi }{3}$
Using, $\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }},\cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }},sec\dfrac{\pi }{3} = 2$, we get,
$= 2 \times {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2} + 2 \times {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2} + 2 \times {\left( 2 \right)^2}$
On squaring we get,
$= {2} \times \dfrac{1}{{{2}}} + {2} \times \dfrac{1}{{{2}}} + 2 \times 4$
On simplification we get,
$= 1 + 1 + 8$
$= 10$
= Right hand side
Therefore, $2{\sin ^2}\dfrac{{3\pi }}{4} + 2{\cos ^2}\dfrac{\pi }{4} + 2{\sec ^2}\dfrac{\pi }{3} = 10$ (proved).

Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.${\sec ^2}x - {\tan ^2}x = 1$
4.${\operatorname{cosec} ^2}x - {\cot ^2}x = 1$
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:

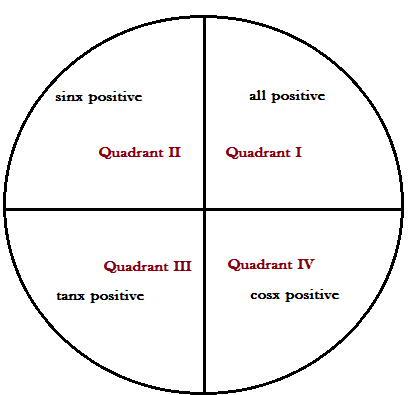
$\sin 2x = 2\sin x\cos x$
$\cos 2x = {\cos ^2}x - {\sin ^2}x = 1 - 2{\sin ^2}x = 2{\cos ^2}x - 1$
$\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}} = \dfrac{2}{{\cot x - \tan x}}$
Also, the trigonometric ratios of the standard angles are given by

| $0^\circ$| $30^\circ$| $45^\circ$| $60^\circ$| $90^\circ$
---|---|---|---|---|---
$\operatorname{Sin} x$| 0| $\dfrac{1}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{{\sqrt 3 }}{2}$ | 1
$\operatorname{Cos} x$| 1| $\dfrac{{\sqrt 3 }}{2}$| $\dfrac{1}{{\sqrt 2 }}$| $\dfrac{1}{2}$| 0
$\operatorname{Tan} x$| 0| $\dfrac{1}{{\sqrt 3 }}$ | 1| $\sqrt 3$| Undefined
$Cotx$| undefined| $\sqrt 3$| 1| $\dfrac{1}{{\sqrt 3 }}$| 0
$\cos ecx$| undefined| 2| $\sqrt 2$| $\dfrac{2}{{\sqrt 3 }}$| 1
$\operatorname{Sec} x$| 1| $\dfrac{2}{{\sqrt 3 }}$| $\sqrt 2$| 2| Undefined