Question
Question: Prove that 1\. \[\dfrac{{\cos A}}{{1 - \sin A}} = \tan \left( {\dfrac{\pi }{4} + \dfrac{A}{2}} \r...
Prove that
1. 1−sinAcosA=tan(4π+2A)
2. sin20∘sin40∘sin60∘sin80∘=163
Solution
In this problem they give the trigonometric relation to prove. We are going to prove this problem by using the method, first consider the left hand side and from that we will derive the right hand side.
Formula used: We have used the following formula to derive the right hand side in i),
Algebraic formula,
a2−b2=(a+b)(a−b)
(a+b)2=a2+2ab+b2
Trigonometric formula,
sin2θ+cos2θ=1
sin2θ=2sinθcosθ
cos2θ=cos2θ−sin2θ
cos θsin θ=tanθ
tan(a+b)=1−(tan a)(tan b)tan a + tan b
We have used the following formula to derive the right hand side in ii),
Trigonometric formula,
2sinxsiny=cos(x−y)−cos(x+y)
2sinxcosy=sin(x+y)+sin(x−y)
sin(−θ)=−sinθ
Complete step-by-step answer:
1. We need to prove 1−sinAcosA=tan(4π+2A).
Let us consider the L.H.S =1−sinAcosA
We will multiply and divide the same term 1+sinA, we get
⇒1−sinAcosA×1+sinA1+sinA
Simplifying we get,
⇒(1−sinA)(1+sinA)cosA(1+sinA)
Using the algebraic formula a2−b2=(a+b)(a−b) for denominator,
⇒(1−sin2A)cosA(1+sinA)
We know, sin2θ+cos2θ=1 by using this,
⇒cos2AcosA(1+sinA)
Simplifying we get,
⇒cosA1+sinA
By using the sin2θ=2sinθcosθ to get the required result,
⇒cos22A−sin22Asin22A+cos22A+2sin2Acos2A
Now, we can use the algebraic formula, (a+b)2=a2+2ab+b2 and the trigonometric formula,cos2θ=cos2θ−sin2θ
⇒(cos2A+sin2A)(cos2A−sin2A)(sin2A+cos2A)2
Cancelling the common terms in numerator and denominator we get,
⇒cos2A−sin2Asin2A+cos2A
Dividing denominator and numerator by cos2A,
⇒cos2Acos2A−sin2Acos2Asin2A+cos2A
By using the formula cos θsin θ=tanθ we get,
⇒1−tan2Atan4πtan2A+tan4π
We know that is tan(a+b)=1−(tan a)(tan b)tan a + tan b which gives,
⇒tan(4π+2A)
=R.H.S.
Hence L.H.S = R.H.S.
∴1−sinAcosA=tan(4π+2A)(proved).
2. We need to prove sin20∘sin40∘sin60∘sin80∘=163
L.H.S =
⇒sin20∘sin40∘sin60∘sin80∘
Multiply and divide by 2 we get,
⇒21(sin20∘sin60∘)(2sin40∘sin80∘)
We know, 2sinxsiny=cos(x−y)−cos(x+y) by using,
⇒21(sin20∘sin60∘)[cos(80∘−40∘)−cos(80∘+40∘)]
Substituting the value sin60∘=23,
⇒21(sin20∘23)(cos40∘−cos120∘)
Simplifying we get,
⇒43sin20∘(cos40∘+21)
Again we can use, 2sinxcosy=sin(x+y)+sin(x−y)
⇒832sin20∘cos40∘+83sin20∘
⇒83[sin(20∘+40∘)+sin(20∘−40∘)]+83sin20∘
Simplifying we get,
⇒83[sin60∘+sin(−20∘)]+83sin20∘
Now, sin(−θ)=−sinθ
⇒83(sin60∘−sin20∘)+83sin20∘
⇒83sin60∘−83sin20∘+83sin20∘
Subtracting the terms and substituting the value of sin60∘=23 we get,
⇒83×23
⇒163
=R.H.S.
L.H.S. = R.H.S.
∴Hence, sin20∘sin40∘sin60∘sin80∘=163(Proved).
Note: Sin Cos formulas are based on sides of the right-angled triangle. Sin and Cos are basic trigonometric functions along with tan function, in trigonometry. Sine of angle is equal to the ratio of opposite side and hypotenuse whereas cosine of an angle is equal to ratio of adjacent side and hypotenuse.
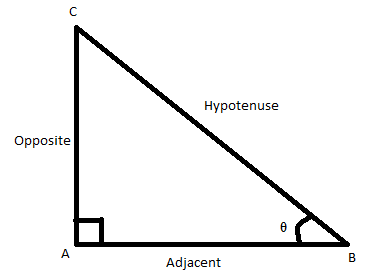
sinθ=HypotenuseOpposite side
cosθ=HypotenuseAdjacent
In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. The most widely used trigonometric functions are the sine, the cosine, and the tangent.
