Question

Prove $\sin \left( {{{90}^ \circ } - a} \right) = \cos a$.

Answer 1

The given problem deals with the basic concepts and formulae of trigonometric functions. The given question requires us to convert the cosine ratio of an angle to sine ratio of its complementary angle. These types of trigonometric identities or formulae can be proved by considering a right angled triangle and then calculating the trigonometric ratios.

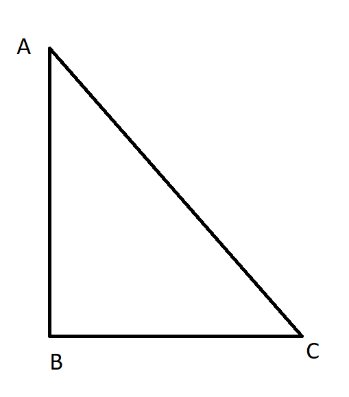
Complete step by step solution:
So, we have to prove the cosine of an angle is equal to the sine of its complementary angle.

Consider a right angled triangle ABC, in which $\angle B = {90^ \circ }$

Then AC = Hypotenuse, AB = Perpendicular for$\angle C$, BC = Base for$\angle C$.

Also AC = Hypotenuse, AB = Base for$\angle A$, BC = Perpendicular for$\angle A$.

Then $\angle A + \angle C = {90^ \circ }$, using angle sum property of a triangle. So, the two angles $\angle A$ and $\angle C$ are complementary angles.

So, $\angle C = {90^ \circ } - \angle A$

Let us assume $\angle A = a$ and $\angle C = c$

Then $c = {90^ \circ } - a$

We know that sine of an angle is equal to $\dfrac{{{\text{Opposite Side}}}}{{{\text{Hypotenuse}}}}$ and cosine of an angle is $\dfrac{{{\text{Adjacent Side}}}}{{{\text{Hypotenuse}}}}$.

Now, $\sin c = \dfrac{{AB}}{{AC}}$ or $\sin ({90^ \circ } - a) = \dfrac{{AB}}{{AC}}$ (AC = Hypotenuse, AB = Perpendicular for$\angle C$)

Also, $\cos a = \dfrac{{AB}}{{AC}}$ (AC = Hypotenuse, AB = Base for$\angle A$)

Thus, $\sin \left( {{{90}^ \circ } - a} \right) = \cos a$

Note: The above problem can be solved by various methods. The easiest way to solve the question is by considering a right angled triangle and calculating trigonometric ratios. The result of the above problem can also be observed and visualised by the help of graphs of trigonometric ratios sine and cosine.