Question

Prove ${\rm{v = }}\;{\rm{u + at}}$
Where u = initial velocity, v = final velocity, a = acceleration and t= time period.

Answer 1

We know that this is the first kinematic equation of motion. When a particle moves in a straight line with constant acceleration, then position, time velocity and acceleration of the particle are represented by equations known as the kinematic equation.

Complete step by step answer:
Consider a velocity-time graph for the positive constant acceleration of a particle. Let u be the initial velocity of the particle at t=0 and v is the final velocity of the particle after time t. Consider two points A and B on the curve corresponding to t=0 and t=t. Draw BD perpendicular on the time axis. Also, draw AC perpendicular on BD.
Therefore, OA = CD = u; BC = (v-u) and OD = t as shown in graph.

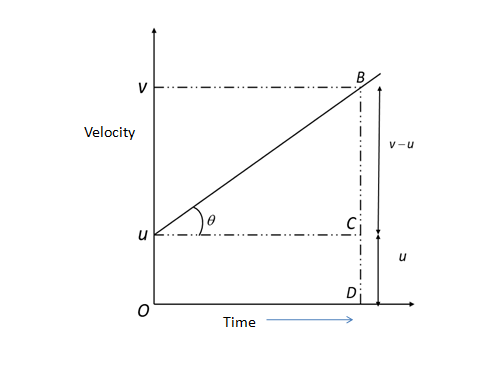
Also acceleration (a) = change in velocity/time taken
According to the graph,
a = slope of v-t graph = $tan\theta\ {\rm{ = }}\dfrac{{{\rm{BC}}}}{{{\rm{AC}}}}\; = \;\dfrac{{{\rm{BC}}}}{{{\rm{OD}}}}$
$\Rightarrow {\rm{v - u = at}}$
$\Rightarrow \;{\rm{v}}\,{\rm{ = u + }}\;{\rm{at}}$

Hence, it is proved by graphical method.

Additional information: This equation represents the relation between velocities, acceleration and time. This equation can be proved by calculus method and by checking dimensional correctness or displacement method.

Note: Here the velocity is defined as rate of change of displacement and it is a vector quantity because it represents magnitude as well as direction and acceleration is defined as the rate of change of velocity with respect to time. It is also a vector quantity. Sometimes the negative acceleration is also called a negative retardation. The unit of velocity is ${\rm{m/s}}$ and the unit represents ${\rm{m/}}{{\rm{s}}^2}$. The dimensional formula of velocity is $\left[ {{\rm{L}}{{\rm{T}}^{ - 1}}} \right]$ and the dimensional formula of acceleration is $\left[ {{\rm{L}}{{\rm{T}}^{ - 2}}} \right]$ .