Question

Prove geometrically that $\cos \left( {x + y} \right) = \cos x\cos y - \sin x\sin y$

Answer 1

This problem deals with trigonometric sum and difference identities. Trigonometric sum and difference identities of cosine formulas are used here which are given below:
$\Rightarrow \cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$
$\Rightarrow \cos \left( {A - B} \right) = \cos A\cos B + \sin A\sin B$
Here the negative angle of cosine is positive which is given by:
$\Rightarrow \cos \left( { - A} \right) = \cos A$

Complete step-by-step answer:
Let there be two points P and Q in the XY plane, as shown in the figure below:
The point P is at an angle x with the horizontal axis and whereas the point Q is at an angle y with the horizontal axis.

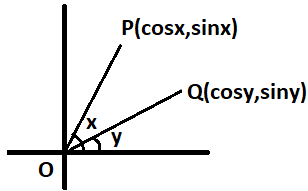
Then the coordinates of the point P are $P = \left( {\cos x,\sin x} \right)$
The coordinates of the point Q are $Q = \left( {\cos y,\sin y} \right)$
Now the distance between the points P and Q is given by PQ, as given below:
$\Rightarrow PQ = \sqrt {{{\left( {\cos x - \cos y} \right)}^2} + {{\left( {\sin x - \sin y} \right)}^2}}$
Squaring the above equation on both sides as given below:
$\Rightarrow P{Q^2} = {\left( {\cos x - \cos y} \right)^2} + {\left( {\sin x - \sin y} \right)^2}$
$\Rightarrow P{Q^2} = {\cos ^2}x + {\cos ^2}y - 2\cos x\cos y + {\sin ^2}x + {\sin ^2}y - 2\sin x\sin y$
On expanding the above expression and further simplification gives:
$\Rightarrow P{Q^2} = {\cos ^2}x + {\sin ^2}x + {\cos ^2}y + {\sin ^2}y - 2\cos x\cos y - 2\sin x\sin y$
$\Rightarrow P{Q^2} = 1 + 1 - 2\left( {\cos x\cos y + \sin x\sin y} \right)$
$\Rightarrow P{Q^2} = 2 - 2\left( {\cos x\cos y + \sin x\sin y} \right)$
We know that $\cos \left( {x - y} \right) = \cos x\cos y + \sin x\sin y$
Hence substitute it in the above $P{Q^2}$ expression as given below:
$\Rightarrow P{Q^2} = 2 - 2\cos \left( {x - y} \right)$
Now equating both the $P{Q^2}$ expressions, as given below:
$\Rightarrow 2 - 2\left( {\cos x\cos y + \sin x\sin y} \right) = 2 - 2\cos \left( {x - y} \right)$
Here 2 gets cancelled on both sides, ad given below:
$\Rightarrow 2\left( {\cos x\cos y + \sin x\sin y} \right) = 2\cos \left( {x - y} \right)$
Here dividing the above equation by 2.
Now substitute $- y$ in place of $y$ , in the above equation as given below:
$\Rightarrow \cos \left( {x - \left( { - y} \right)} \right) = \left( {\cos x\cos \left( { - y} \right) + \sin x\sin \left( { - y} \right)} \right)$
$\Rightarrow \cos \left( {x + y} \right) = \left( {\cos x\cos y + \sin x\left( { - \sin y} \right)} \right)$
$\therefore \cos \left( {x + y} \right) = \left( {\cos x\cos y - \sin x\sin y} \right)$

Hence proved.

Note:
Please note that while solving the problem, we should understand that only the cosine and secant trigonometric ratios of negative angles is positive, all the other trigonometric ratios of negative angles are negative. Which is given by:
$\Rightarrow \sin \left( { - \theta } \right) = - \sin \theta$
$\Rightarrow \cos \left( { - \theta } \right) = \cos \theta$
$\Rightarrow \tan \left( { - \theta } \right) = - \tan \theta$
$\Rightarrow \cot \left( { - \theta } \right) = - \cot \theta$
$\Rightarrow \sec \left( { - \theta } \right) = \sec \theta$
$\Rightarrow \cos ec\left( { - \theta } \right) = - \cos ec\theta$