Solveeit Logo
Login

Question

Question: Prove geometrically that: \( \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B \)...

Prove geometrically that:
cos⁡(A+B)=cos⁡Acos⁡B−sin⁡Asin⁡B\cos \left( A+B \right)=\cos A\cos B-\sin A\sin B

Explanation

Solution

In a right-angled triangle with length of the side opposite to angle θ as perpendicular (P), base (B) and hypotenuse (H):
sin⁡θ=PH,cos⁡θ=BH,tan⁡θ=PB\sin \theta =\dfrac{P}{H},\cos \theta =\dfrac{B}{H},\tan \theta =\dfrac{P}{B}
P2+B2=H2{{P}^{2}}+{{B}^{2}}={{H}^{2}} (Pythagoras' Theorem)
Draw a right-angled ΔPQR\Delta PQR with ∠Q=90∘\angle Q={{90}^{\circ }} and ∠P=A\angle P=A . At the point P, draw another right-angled triangle ΔPRS\Delta PRS on the hypotenuse of ΔPQR\Delta PQR , such that ∠R=90∘\angle R={{90}^{\circ }} and ∠P=B\angle P=B . Finally, drop a line ST perpendicular on PQ to complete a right-angled triangle ΔPTS\Delta PTS with ∠T=90∘\angle T={{90}^{\circ }} and ∠P=A+B\angle P=A+B , and complete the proof by considering the lengths of the sides of the triangles. Also draw RM⊥STRM\bot ST .

Complete step-by-step answer:
To prove: cos⁡(A+B)=cos⁡Acos⁡B−sin⁡Asin⁡B\cos \left( A+B \right)=\cos A\cos B-\sin A\sin B .

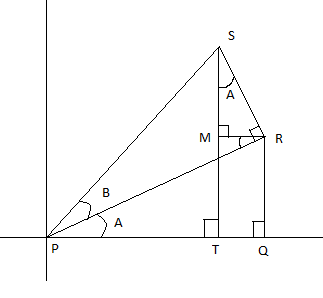
Proof: Using the definition of trigonometric ratios:
In ΔPQR\Delta PQR :
cos⁡A=PQPR\cos A=\dfrac{PQ}{PR} ... (1).
In ΔPRS\Delta PRS :
cos⁡B=PRPS\cos B=\dfrac{PR}{PS} ... (2).
sin⁡B=SRPS\sin B=\dfrac{SR}{PS} ... (3).
Since MR∥PQMR\parallel PQ , ∠MRP=∠PRQ=A\angle MRP=\angle PRQ=A (Alternate interior angles), and so ∠MRS=90∘−A\angle MRS={{90}^{\circ }}-A .
∴ In ΔSMR\Delta SMR , ∠MSR=90∘−(90∘−A)=A\angle MSR={{90}^{\circ }}-({{90}^{\circ }}-A)=A , and:
sin⁡A=RMSR\sin A=\dfrac{RM}{SR} ... (4).
Now, using equations (1) and (2), we get:
cos⁡A.cos⁡B=PQPR.PRPS=PQPS\cos A.\cos B=\dfrac{PQ}{PR}.\dfrac{PR}{PS}=\dfrac{PQ}{PS} ... (5).
Finally, in ΔPTS\Delta PTS :
cos⁡(A+B)=PTPS=PQ−QTPS\cos (A+B)=\dfrac{PT}{PS}=\dfrac{PQ-QT}{PS}
Since QT = MR, we can write:
cos⁡(A+B)=PQPS−RMPS\cos (A+B)=\dfrac{PQ}{PS}-\dfrac{RM}{PS}
⇒ cos⁡(A+B)=PQPS−RMSR.SRPS\cos (A+B)=\dfrac{PQ}{PS}-\dfrac{RM}{SR}.\dfrac{SR}{PS}
Using equations (3), (4) and (5):
cos⁡(A+B)=cos⁡Acos⁡B−sin⁡Asin⁡B\cos \left( A+B \right)=\cos A\cos B-\sin A\sin B

Note: Using the fact that cos⁡(−θ)=cos⁡θ\cos (-\theta )=\cos \theta and sin⁡(−θ)=−sin⁡θ\sin (-\theta )=-\sin \theta , we will get:
cos⁡(A−B)=cos⁡Acos⁡B+sin⁡Asin⁡B\cos \left( A-B \right)=\cos A\cos B+\sin A\sin B
Similar strategy can be applied to prove results for sin⁡(A±B)\sin (A\pm B) .
There are many other ways to prove the result: using a unit circle, other types of constructions, etc.