Question

Prove $\cos \left( {\dfrac{{3\pi }}{2} + x} \right)\cos \left( {2\pi + x} \right)\left[ {\cot \left( {\dfrac{{3\pi }}{2} - x} \right)\cot \left( {2\pi + x} \right)} \right] = 1$.

Answer 1

Hint : Here, in the given question, we need to prove that $\cos \left( {\dfrac{{3\pi }}{2} + x} \right)\cos \left( {2\pi + x} \right)\left[ {\cot \left( {\dfrac{{3\pi }}{2} - x} \right)\cot \left( {2\pi + x} \right)} \right] = 1$. Here we are given a trigonometric function, we need to know how a function can be represented in terms of other functions so that we can simplify and prove the given function. For the given question, first we will solve the given functions individually and try to convert them into the simplest form using identities. After this, we will try to represent the $\cot$ function in terms of $\cos$ and after that we will simplify the given function to prove that LHS is equal to RHS.

Complete step-by-step answer :
To prove: $\cos \left( {\dfrac{{3\pi }}{2} + x} \right)\cos \left( {2\pi + x} \right)\left[ {\cot \left( {\dfrac{{3\pi }}{2} - x} \right)\cot \left( {2\pi + x} \right)} \right] = 1$.
L.H.S. = $\cos \left( {\dfrac{{3\pi }}{2} + x} \right)\cos \left( {2\pi + x} \right)\left[ {\cot \left( {\dfrac{{3\pi }}{2} - x} \right)\cot \left( {2\pi + x} \right)} \right]$
First we will solve, $\cos \left( {\dfrac{{3\pi }}{2} + x} \right)$
Putting $\pi = 180^\circ$, we get
$= \cos \left( {\dfrac{{3 \times 180^\circ }}{2} + x} \right)$
On simplification, we get
$= \cos \left( {270^\circ + x} \right)$
It can also be written as,
$= \cos \left( {360^\circ - 90^\circ + x} \right)$
As we know $360^\circ = 2\pi$, we get
$= \cos \left( {2\pi + \left( {x - 90^\circ } \right)} \right)$
As we know $\cos \left( {2\pi + x} \right) = \cos x$. Therefore, we get
$= \cos \left( {x - 90^\circ } \right)$
On taking negative sign as common, we get
$= \cos \left( { - \left( {90^\circ - x} \right)} \right)$
As we know $\cos \left( { - x} \right) = \cos x$. Therefore, we get
$= \cos \left( {90^\circ - x} \right)$
As we know $\cos \left( {90^\circ - \theta } \right) = \sin \theta$ (Here, $\sin$ is positive because $90^\circ - \theta$ lies in the first quadrant, and in first quadrant$\sin$ is positive). Therefore, we get
Therefore, we get
$= \sin x$
Now, $\cos \left( {2\pi + x} \right) = \cos x$
Now we solve, $\cot \left( {\dfrac{{3\pi }}{2} - x} \right)$
Putting $\pi = 180^\circ$
$= \cot \left( {\dfrac{{3 \times 180^\circ }}{2} - x} \right)$
On simplification, we get
$= \cot \left( {270^\circ - x} \right)$
It can also be written as,
$= \cot \left( {360^\circ - 90^\circ - x} \right)$
As we know $360^\circ = 2\pi$, we get
$= \cot \left( {2\pi - 90^\circ - x} \right)$
On taking negative sign as common, w get
$= \cot \left( {2\pi - \left( {x + 90^\circ } \right)} \right)$
As we know $\cot \left( {2\pi - x} \right) = - \cot x$. Therefore, we get
$= - \cot \left( {x + 90^\circ } \right)$
As we know $\cot \left( {90^\circ + \theta } \right) = - \tan \theta$ (Here, $\tan$ is negative because $90^\circ + \theta$ lies in the second quadrant, and in second quadrant $\tan$ is negative). Therefore, we get
$= - \left( { - \tan x} \right)$
$= \tan x$
Now, $\cot \left( {2\pi + x} \right) = \cot x$
Putting these values in the equation
$\cos \left( {\dfrac{{3\pi }}{2} + x} \right)\cos \left( {2\pi + x} \right)\left[ {\cot \left( {\dfrac{{3\pi }}{2} - x} \right)\cot \left( {2\pi + x} \right)} \right]$
$= \left( {\sin x} \right) \times \left( {\cos x} \right) \times \left[ {\tan x + \cot x} \right]$
Now, we will represent $\tan$ and $\cot$ in terms of $\sin$ and $\cos$. As we know $\tan x = \dfrac{{\sin x}}{{\cos x}}$ and $\cot x = \dfrac{{\cos x}}{{\sin x}}$. Therefore, we get
$= \left( {\sin x\cos x} \right) \times \left[ {\dfrac{{\sin x}}{{\cos x}} + \dfrac{{\cos x}}{{\sin x}}} \right]$
On taking LCM, we get
$= = \left( {\sin x\cos x} \right) \times \left[ {\dfrac{{\sin x \times \sin x + \cos x \times \cos x}}{{\cos x\sin x}}} \right]$
$= \left( {\sin x\cos x} \right) \times \left[ {\dfrac{{{{\sin }^2}x + {{\cos }^2}x}}{{\sin x\cos x}}} \right]$
As we know that ${\sin ^2}x + {\cos ^2}x = 1$, thus we get
$= \left( {\sin x\cos x} \right) \times \left[ {\dfrac{1}{{\sin x\cos x}}} \right]$
On multiplication, we get
$= \dfrac{{\sin x\cos x}}{{\sin x\cos x}}$
On cancelling out common terms, we get
$= 1$
= R.H.S.
Hence proved.

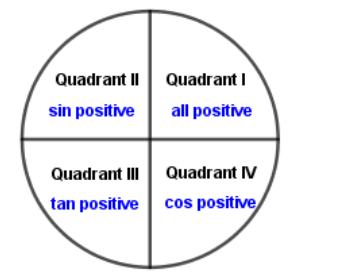
Note : To solve the questions related to trigonometric functions, one must remember all the standard formulas of trigonometric functions. Most of the trigonometric functions questions are just based on substitutions, we can only solve the problem if we know the formulas and sign convention. We should know signs of trigonometric ratios in different quadrants. The easiest way to memorise the signs of trigonometric ratios in different quadrants is the four-word phrase ‘ALL SCHOOL TO COLLEGE’. The first letter of the first word in the phrase is A, indicating that all trigonometric ratios are positive in the first quadrant. The first letter of the second word in the phrase is S, indicates that $\sin e$ and its reciprocal is positive in the second quadrant. The first letter of the third word in the phrase is T, indicates that $\tan gent$ and its reciprocal is positive in the third quadrant. The first letter of the fourth word in the phrase is C, indicates that $\cos ine$ and its reciprocal is positive in the fourth quadrant.